Пусть за х дней по плану токарь выполняет задание.
Тогда, 8х деталей – будет объем работы токаря за х дней.
8 +(10-8) = 10 деталей - будет производительность труда токаря по факту.
(х-1) дней – это фактическое время на выполнение задания.
Получим уравнение:
10 (х-1) - 20 = 8х
10х – 10 - 20 = 8х
2х=30
Х = 15 дней, т.е. за 15 дней по плану токарь должен выполнить задание.
8Х = 8*15= 120 деталей, т.е. такова производительность труда токаря при перевыполнении плана.
120+20= 140 деталей изготовил токарь.
ответ: 65 км/ч
Объяснение:
1) 312 : 2 = 156 (км) - половина расстояния
2) 12 мин = 12/60 ч = 1/5 ч
Скорость Время Расстояние
До остановки x - 5 156
После ост. x 156
Время до остановки на 12 мин больше времени после остановки:
х > 5 по смыслу задачи, поэтому умножим обе части уравнения на
5x(x - 5):
780x - 780(x - 5) = x(x - 5)
780x - 780x + 3900 = x² - 5x
x² - 5x - 3900 = 0
По теореме Виета:
x₁ · x₂ = - 3900
x₁ + x₂ = 5
Значит, x₁ = - 60 - не подходит по смыслу задачи
x₂ = 65
Пусть за х дней по плану токарь выполняет задание.
Тогда, 8х деталей – будет объем работы токаря за х дней.
8 +(10-8) = 10 деталей - будет производительность труда токаря по факту.
(х-1) дней – это фактическое время на выполнение задания.
Получим уравнение:
10 (х-1) - 20 = 8х
10х – 10 - 20 = 8х
2х=30
Х = 15 дней, т.е. за 15 дней по плану токарь должен выполнить задание.
8Х = 8*15= 120 деталей, т.е. такова производительность труда токаря при перевыполнении плана.
120+20= 140 деталей изготовил токарь.
ответ: 65 км/ч
Объяснение:
1) 312 : 2 = 156 (км) - половина расстояния
2) 12 мин = 12/60 ч = 1/5 ч
Скорость Время Расстояние
До остановки x - 5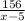 156
156
После ост. x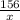 156
156
Время до остановки на 12 мин больше времени после остановки:
х > 5 по смыслу задачи, поэтому умножим обе части уравнения на
5x(x - 5):
780x - 780(x - 5) = x(x - 5)
780x - 780x + 3900 = x² - 5x
x² - 5x - 3900 = 0
По теореме Виета:
x₁ · x₂ = - 3900
x₁ + x₂ = 5
Значит, x₁ = - 60 - не подходит по смыслу задачи
x₂ = 65
ответ: 65 км/ч