5
Объяснение:
Сумма всех чисел от 1 до n равна
Для искомой суммы должно выполняться два условия:
Или
Для первого неравенства n принадлежит интервалам
∪
Для второго неравенства n принадлежит отрезкам
Их пересечение
Единственное натуральное число из данного промежутка 14.
Значит исходная сумма была 14*15/2=105, на потерянной карточке было написано 5
5
Объяснение:
Сумма всех чисел от 1 до n равна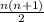
Для искомой суммы должно выполняться два условия:
Или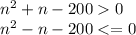
Для первого неравенства n принадлежит интервалам
Для второго неравенства n принадлежит отрезкам
Их пересечение![(\frac{-1+3\sqrt{89}}{2},\frac{1+3\sqrt{89}}{2}]](/tpl/images/1430/2598/445ec.png)
Единственное натуральное число из данного промежутка 14.
Значит исходная сумма была 14*15/2=105, на потерянной карточке было написано 5