Пусть первый сплав весит х кг - тогда чистого олова в нем 0.05*х
Тогда второй сплав весит (х+6)- тогда чистого олова в нем 0.11*(х+6)
Тогда третий сплав весит х+х+6=2х+6- тогда чистого олова в нем
0.1*(2х+6).
Поскольку из двух первых сплавово получили третий, то при переплавке олово никуда дется не могло . Поэтому сумма олова в первых двух сплавах равно весу олова в третьем сплаве. То есть:
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2)
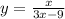. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б)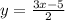
при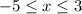 
Если x = -5, то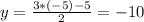
Если х= 3, то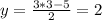
Значит,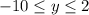
9 кг
Объяснение:
Пусть первый сплав весит х кг - тогда чистого олова в нем 0.05*х
Тогда второй сплав весит (х+6)- тогда чистого олова в нем 0.11*(х+6)
Тогда третий сплав весит х+х+6=2х+6- тогда чистого олова в нем
0.1*(2х+6).
Поскольку из двух первых сплавово получили третий, то при переплавке олово никуда дется не могло . Поэтому сумма олова в первых двух сплавах равно весу олова в третьем сплаве. То есть:
0.05*х+0.11*(х+6)=0.1*(2х+6)
Решаем полученное уравнение
0.05*х+0.11*х+0.66=0.2*х+0.6
0.16*х+0.66=0.2*х+0.6
0.06=0.04*х
х=1.5 кг
Тогда масса третьего сплава = 2*1.5+6=9 кг