Как и в предыдущей твоей задаче, комплексное число a+bi можно рассматривать как вектор . Как видно из сложения векторов по правилу параллелограмма, сумма двух векторов, имеющих общее начало, является диагональю параллелограмма, двумя сторонами которого являются начальные векторы. Диагональ параллелограмма — это биссектриса его угла. Значит, конец любого вектора, лежащего на луче, продолжающем диагональ параллелограмма, подходит для ответа.
d = 6+8i + 4-3i = 10 + 5i
Вектор v, соответствующий d — (10; 5). Любая точка (n;m) такая, что существует такое неотрицательное число k такое, что k*d = (n;m), лежит на биссектрисе.
Решим систему уравнений методом математического сложения. Запишем систему:
3х - 2у = 8;
6х + 3у = 9.
Домножим первое уравнение системы на - 2, получим систему:
- 6х + 4у = - 16;
6х + 3у = 9.
Сложим уравнения и получим систему:
3х - 2у = 8;
4у + 3у = 9 - 16;
Система:
3х - 2у = 8;
7у = - 7.
Система:
3х - 2у = 8;
у = -1.
Подставляем в первое уравнение системы у = - 1 и находим значение х:
3х + 2 = 8;
у = - 1.
Система:
3х = 6;
у = - 1.
Система:
х = 2;
у = - 1.
ответ: решение системы уравнений (2; - 1)..
Как и в предыдущей твоей задаче, комплексное число a+bi можно рассматривать как вектор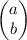 . Как видно из сложения векторов по правилу параллелограмма, сумма двух векторов, имеющих общее начало, является диагональю параллелограмма, двумя сторонами которого являются начальные векторы. Диагональ параллелограмма — это биссектриса его угла. Значит, конец любого вектора, лежащего на луче, продолжающем диагональ параллелограмма, подходит для ответа.
. Как видно из сложения векторов по правилу параллелограмма, сумма двух векторов, имеющих общее начало, является диагональю параллелограмма, двумя сторонами которого являются начальные векторы. Диагональ параллелограмма — это биссектриса его угла. Значит, конец любого вектора, лежащего на луче, продолжающем диагональ параллелограмма, подходит для ответа.
d = 6+8i + 4-3i = 10 + 5i
Вектор v, соответствующий d — (10; 5). Любая точка (n;m) такая, что существует такое неотрицательное число k такое, что k*d = (n;m), лежит на биссектрисе.
Таким образом, n/m = 10/5 = 2.
ответ: {(n+mi) | n/m = 2}