Sin(3x)*cos(2x)=sin(5x)​

Вертикальные асимптоты:  x = 2

Горизонтальные асимптоты:  y = 3

Нет наклонных асимптот

Объяснение:

Выясним, при каких значениях переменной функция  3 x + 1 x − 2  не определена. x = 2

Рассмотрим рациональную функцию  

, где  n - степень числителя, а  m - степень знаменателя.

1. Если  n < m , то ось x,  y = 0 , является горизонтальной асимптотой.

2. Если  n = m , то горизонтальной асимптотой является прямая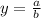

Если  n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).

Найдем  n  и  m

n = 1 ; m = 1

Поскольку  n = m , горизонтальная асимптота является прямой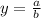  , где  a = 3  и  b = 1

y = 3

Наклонных асимптот нет, поскольку степень числителя меньше либо равна степени знаменателя.

Это множество всех асимптот.

Вертикальные асимптоты:  x = 2

Горизонтальные асимптоты:  y = 3

Нет наклонных асимптот

1) для того чтобы функция была непрерывной, нужно чтобы пределы слева и справа в точках 0 и 1 были равны. Найдем их:

Так как 1≠-∞, то точка 0- это точка разрыва(второго рода).

Чтобы функция была неразрывной в точке 1, нужно чтобы предел от 3-ax^2 был равен 2, так как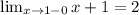

При x=1 ⇒y=2.

Подставим координаты (1;2)  в формулу y=3-ax^2⇒2=3-а⇒а=1, то есть уравнение имеет вид y=3-x^2. Проверим это: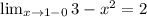

Действительно 2=2, значит функция не будет являться непрерывной в точке 1.

ответ: х=0 - точка разрыва. функция непрерывна в точке х=1 при а=1

2)  Аналогично:

3≠-1, значит -1- это точка разрыва.

В точке x=1 ⇒y=1. Подставим: 1=a*1⇒a=1.

Проверим: .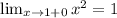

Так как точка  х=0 лежит в области определения функции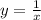 , а из ОДЗ следует что х≠0, то функция также будет прерываться в точке х=0

ответ: х=-1 - точка разрыва,  х=0- точка разрыва, функция будет непрерывна в точке х=1 при а=1