Объяснение:
5.
20 минут=1/3 часа.
Пусть скорость первого велосипедиста - х, а второго - у. ⇒
y₁=10 y₂=-12 ∉. ⇒
x=10+2=12.
ответ: скорость первого велосипедиста - 12 км/ч,
скорость второго велосипедиста - 10 км/ч.
Пусть скорость первого велосипедиста - Х км/ч, тогда скорость второго Х-2. Путь у обоих 20км. Время первого велосипедиста 20/х, второго 20/(х-2).
Так ка мы знаем, что первый пришел раньше второго на 20 минут (1/3 часа), составляем уравнение:
20/х = 20(х-2) + 1/3, х не = 0
3(20х - 40 - 20х) = - 2х
- 2х -120 = 0
Решаем через дискриминант
D = 4 + 4*120 = 484
х1 = (2-22)/2 = -10 - не подходит, так ка скорость не может быть отрицательна
х2 = (2+22)/2=12
Следовательно скорость первого велосипедиста 12км/ч, а второго 10км/ч
Объяснение:
5.
20 минут=1/3 часа.
Пусть скорость первого велосипедиста - х, а второго - у. ⇒
y₁=10 y₂=-12 ∉. ⇒
x=10+2=12.
ответ: скорость первого велосипедиста - 12 км/ч,
скорость второго велосипедиста - 10 км/ч.
Пусть скорость первого велосипедиста - Х км/ч, тогда скорость второго Х-2. Путь у обоих 20км. Время первого велосипедиста 20/х, второго 20/(х-2).
Так ка мы знаем, что первый пришел раньше второго на 20 минут (1/3 часа), составляем уравнение:
20/х = 20(х-2) + 1/3, х не = 0
3(20х - 40 - 20х) =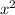 - 2х
- 2х
Решаем через дискриминант
D = 4 + 4*120 = 484
х1 = (2-22)/2 = -10 - не подходит, так ка скорость не может быть отрицательна
х2 = (2+22)/2=12
Следовательно скорость первого велосипедиста 12км/ч, а второго 10км/ч