|x²-x+5|-|x+5|-3 = 0
1)x²-x+5
D = b²-4ac = 1-20 = -19 < 0
Квадратный трёхчлен строго положителен, поэтому знак модуля можем убрать
x²-x+5-3-|x+5| = 0
x²-x+2-|x+5| = 0
2)x >= -5
x²-x+2-(x+5) = 0
x²-x+2-x-5 = 0
x²-2x-3 = 0
Теорема Виета:
{x1+x2 = 2
{x1•x2 = -3
x1 = 3
x2 = -1
2)x < -5
x²-x+2+x+5 = 0
x²+7 = 0
x² ≠ +7
∅
ответ: {-1; 3}
-1 и 3
Объяснение:
Заметим, что:
Тогда перепишем уравнение:
Раскроем модуль:
Так как оба корня больше -5, они оба подходят.
Уравнение не имеет корней.
Тогда ответом будут 2 числа: -1 и 3.
Уравнение решено!
Приведу другой решения:
(если вы увидели, что у дискриминант отрицательный и не поняли, что с этим делать)
Так как оба корня больше -8 и -5, то берем их в ответ.
Здесь нет корней.
Тогда ответом будут числа -1 и 3.
|x²-x+5|-|x+5|-3 = 0
1)x²-x+5
D = b²-4ac = 1-20 = -19 < 0
Квадратный трёхчлен строго положителен, поэтому знак модуля можем убрать
x²-x+5-3-|x+5| = 0
x²-x+2-|x+5| = 0
2)x >= -5
x²-x+2-(x+5) = 0
x²-x+2-x-5 = 0
x²-2x-3 = 0
Теорема Виета:
{x1+x2 = 2
{x1•x2 = -3
x1 = 3
x2 = -1
2)x < -5
x²-x+2+x+5 = 0
x²+7 = 0
x² ≠ +7
∅
ответ: {-1; 3}
-1 и 3
Объяснение:
Заметим, что:
Тогда перепишем уравнение:
Раскроем модуль:
Так как оба корня больше -5, они оба подходят.
Уравнение не имеет корней.
Тогда ответом будут 2 числа: -1 и 3.
Уравнение решено!
Приведу другой решения:
(если вы увидели, что у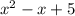
дискриминант отрицательный и не поняли, что с этим делать)
Так как оба корня больше -8 и -5, то берем их в ответ.
Здесь нет корней.
Здесь нет корней.
Здесь нет корней.
Тогда ответом будут числа -1 и 3.
Уравнение решено!