метод интервалов:
1.
-x²+19x-84=0. D=19²-4*(-1)*(-84)=361-336=25
x₁=7, x₂=12
x-6≠0. x≠6
2.
++++++(6)---------[7]+++++++[12]---------->x
3. x>6, x≤7, x≥12
ответ: х принадлежит (6;7] u [12;∞)
метод интервалов:
1.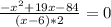
-x²+19x-84=0. D=19²-4*(-1)*(-84)=361-336=25
x₁=7, x₂=12
x-6≠0. x≠6
2.
++++++(6)---------[7]+++++++[12]---------->x
3. x>6, x≤7, x≥12
ответ: х принадлежит (6;7] u [12;∞)