Алгебра: Решить уравнение, 4^(x)+x*2^(x+1)=2^(x-1)+14*2^(x)+x-7

Решить уравнение, 4^(x)+x2^(x+1)=2^(x-1)+142^(x)+x-7

Показать ответ

Ответ:

Kaaaaakkkktus

02.10.2020 05:40

$4^x+x\cdot 2^{x+1}=2^{x-1}+14\cdot 2^x+x-7; 2^{2x}+(2x-\frac{1}{2}-14)\cdot 2^x+7-x=0;$

$2^x=t0; t^2+\frac{4x-29}{2}\cdot t+7-x=0;$

домножим уравнение на 4 и сделаем замену 2t=p>0:

p^2+(4x-29)p+28-4x=0 - квадратное уравнение относительно p; в принципе можно решать с дискриминанта, но числа не самые простые, поэтому идти по этому пути лень. Пытаемся угадать одно из решений и без труда его находим: p=1. Дальнейшее элементарно: по теореме Виета произведение корней равно 28-4x, а раз первый корень p=1, то второй равен p=28-4x.

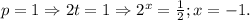
1-й случай $p=1\Rightarrow 2t=1\Rightarrow 2^x=\frac{1}{2}; x=-1.$

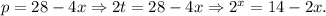
2-й случай. $p=28-4x\Rightarrow 2t=28-4x\Rightarrow 2^x=14-2x.$

Решение x= 3 легко угадывается (8=8), других решений быть не может, поскольку функция, стоящая в левой части уравнения, возрастает, а функция, стоящая в правой части уравнения, убывает.

ответ: - 1; 3

0,0(0 оценок)

Ответ:

Kpoper772

02.10.2020 05:40

$4^x+x\cdot 2^{x+1}=2^{x-1}+14\cdot 2^x+x-7\\ \\ 2^{2x}+2x\cdot 2^x-0.5\cdot 2^x-14\cdot 2^x-x+7=0\\\\ 0.5(2\cdot 2^{2x}+4x\cdot2^x-29\cdot 2^x-2x+14)=0\\ \\ 2\cdot 2^{2x}+4x\cdot 2^x-29\cdot 2^x-2x+14=0$

Решим это уравнение методом разложения на множители

$x(4\cdot2^x-2)+\underbrace{2\cdot 2^{2x}-29\cdot 2^{2x}+14}_{(2\cdot 2^x-1)(2^x-14)}=0\\ \\ 2x(2\cdot 2^x-1)+(2\cdot 2^x-1)(2^x-14)=0\\ \\ (2\cdot 2^x-1)(2x+2^x-14)=0$

Произведение двух множителей равно нолю, значит

$2\cdot 2^x-1=0~~~\Rightarrow~~~ 2^x=0.5~~~\Rightarrow~~~ 2^x=2^{-1}~~~\Rightarrow~~~ \boxed{x_1=-1}\\ \\ 2x+2^x=14$

Левая часть y = 2x + 2ˣ — возрастающая функция (как сумма двух возрастающих функций). С прямой f(x) = 14 функция y = 2x + 2ˣ имеет одну общую точку (3;14). Откуда x₂ = 3 - корень уравнения.

ответ: -1; 3.

0,0(0 оценок)

Популярные вопросы: Алгебра