1. Произведение чисел, переменных и их степеней называется одночленом. Пример: 3⋅5=(3⋅5)⋅(⋅)=152 2. Если в одночлене первым записан числовой множитель, а произведение одинаковых степеней переменных записано в виде одной степени, то такой вид одночлена называют стандартным видом. Пример: 10⋅12=5⋅2⋅123=53 . 3. Числовой множитель одночлена, записанного в стандартном виде, называется коэффициентом одночлена. Степенью одночлена называется сумма показателей степеней всех переменных. Пример: Коэффициент одночлена 53 равен 5, 6 — одночлен первой степени (переменная в первой степени); 4. Чтобы умножить одночлен на одночлен, нужно перемножить их численные коэффициенты, показатели степеней одинаковых переменных сложить, а переменные, входящие в состав только одного из множителей, перенести в произведение без каких-либо изменений. 5. Многочленом называется сумма одночленов. Пример: 32 −7 . 6. Одночлены, у которых произведения переменных равны, хотя их порядок может отличаться, называются подобными одночленами. Пример: 3х^2у 7. Многочлены, содержащие в своей записи подобные члены, с тождественных преобразований могут быть приведены к виду, в котором не будет подобных членов. Такое преобразование многочлена называется приведением подобных членов. 8. Степенью многочлена от нескольких переменных называют наивысшую степень входящих в него одночленов. 9. Многочлен стандартного вида – это многочлен, все члены которого являются одночленами стандартного вида, среди которых нет подобных членов. 10, 11. Для осуществления действия сложения или вычитания многочленов, необходимо:
записать сумму или разность многочленов в зависимости от поставленной задачи; в записанном выражении произвести раскрытие скобок, результатом чего станет многочлен; привести полученный во втором шаге многочлен в стандартный вид. 12. Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Пример: a ⋅ b + c = a ⋅ b + a ⋅ c. 13. Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. 14. Пример вынесения общего множителя за скобки: +=(+). Пример группировки: 3−52−3+152
Группируем члены парами, получаем: (3−52)−(3−152)
2(−5)−3(−5)
(2−3)(−5) 15. Чтобы умножить многочлен на многочлен, нужно: каждый одночлен первого многочлена умножить на каждый одночлен второго многочлена; полученные произведения сложить (то есть записать друг за другом с учетом знаков полученных при умножении). Пример: (a − b)(−a − 2) = a · (−a) − 2a + ab + 2b = −a2 − 2a + ab + 2b
1 шаг. Проверим справедливость утверждения при n=1:
- верно
2 шаг. Предположим, что при n=k следующее утверждение верно:
3 шаг. Докажем, что при n=k+1 следующее утверждение также будет верно:
Для доказательства выполним преобразования:
Рассмотрим получавшуюся сумму. Первое слагаемое делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
Мы получили, что выражение дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение кратно 3.
Возвращаясь к выражению , повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.
2. Если в одночлене первым записан числовой множитель, а произведение одинаковых степеней переменных записано в виде одной степени, то такой вид одночлена называют стандартным видом. Пример: 10⋅12=5⋅2⋅123=53 .
3. Числовой множитель одночлена, записанного в стандартном виде, называется коэффициентом одночлена. Степенью одночлена называется сумма показателей степеней всех переменных. Пример: Коэффициент одночлена 53 равен 5, 6 — одночлен первой степени (переменная в первой степени);
4. Чтобы умножить одночлен на одночлен, нужно перемножить их численные коэффициенты, показатели степеней одинаковых переменных сложить, а переменные, входящие в состав только одного из множителей, перенести в произведение без каких-либо изменений.
5. Многочленом называется сумма одночленов. Пример: 32 −7 .
6. Одночлены, у которых произведения переменных равны, хотя их порядок может отличаться, называются подобными одночленами. Пример: 3х^2у
7. Многочлены, содержащие в своей записи подобные члены, с тождественных преобразований могут быть приведены к виду, в котором не будет подобных членов. Такое преобразование многочлена называется приведением подобных членов.
8. Степенью многочлена от нескольких переменных называют наивысшую степень входящих в него одночленов.
9. Многочлен стандартного вида – это многочлен, все члены которого являются одночленами стандартного вида, среди которых нет подобных членов.
10, 11. Для осуществления действия сложения или вычитания многочленов, необходимо:
записать сумму или разность многочленов в зависимости от поставленной задачи;
в записанном выражении произвести раскрытие скобок, результатом чего станет многочлен;
привести полученный во втором шаге многочлен в стандартный вид.
12. Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Пример: a ⋅ b + c = a ⋅ b + a ⋅ c.
13. Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей.
14. Пример вынесения общего множителя за скобки: +=(+). Пример группировки: 3−52−3+152
Группируем члены парами, получаем:
(3−52)−(3−152)
2(−5)−3(−5)
(2−3)(−5)
15. Чтобы умножить многочлен на многочлен, нужно:
каждый одночлен первого многочлена умножить на каждый одночлен второго многочлена;
полученные произведения сложить (то есть записать друг за другом с учетом знаков полученных при умножении).
Пример: (a − b)(−a − 2) = a · (−a) − 2a + ab + 2b = −a2 − 2a + ab + 2b
Источник: https://math-prosto.ru
1 шаг. Проверим справедливость утверждения при n=1:
2 шаг. Предположим, что при n=k следующее утверждение верно:
3 шаг. Докажем, что при n=k+1 следующее утверждение также будет верно:
Для доказательства выполним преобразования:
Рассмотрим получавшуюся сумму. Первое слагаемое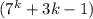 делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом
делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом 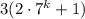 первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
Мы получили, что выражение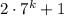 дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение
дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение 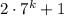 кратно 3.
кратно 3.
Возвращаясь к выражению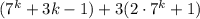 , повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.
, повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.