Показательная функция с основанием 5 > 1 возрастает.
при x = 6
При x ≠ 6
(x-6)²≥0
значит знаменатель
⇒
О т в е т. { 6}
Показательная функция с основанием 5 > 1 возрастает.
При x ≠ 6
(x-6)²≥0
значит знаменатель
О т в е т.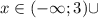 { 6}
{ 6}