1) y' = y³x
Проинтегрируем обе части:
- общее решение дифф. уравнения.
Из начального условия y(1)=1 найдем частное решение:
Подставив в общее решение, найдем С
-1/2 = 1/2 + С ⇔ С = -1/4
- частное решение дифф. уравнения.
2)
Для начала найдем общее решение однородного дифф. уравнения
Проинтегрировав, получим:
ln|y|=3ln|x| + lnC
y = Cx³ - общее решение однородного дифф. уравнения
y = C(x)x³ подставим в наше дифф. уравнение
- общее решение дифф. уравнения
Из начального условия y(1) = e найдем C₁
C₁ = 0
- частное решение дифф. уравнения
1) Найти наибольшее значение функции
y = 1 - log₉ 3^(-x) на отрезке [-1; 5]
Преобразуем функцию
y = 1 - 0,5log₃ 3^(-x)
y = 1 + 0,5х·log₃ 3
y = 1 + 0,5х
находим производную:
y' = 0,5
Производна всегда больше нуля, следовательно, функция у возрастает.
Наибольшее значение находится на правом краю интервала [-1; 5], т.к при х = 5.
у наиб = у(5) = y = 1 + 0,5·5 = 3,5
2) Решить уравнение: 13^(5x-1) · 17^(2x-2) = 13^(3x+1).
17^(2x-2) = 13^(3x+1): 13^(5x-1)
17^(2x-2) = 13^(-2x+2)
17^(2x-2) = 1/13^(2x-2)
(17·13)^(2x-2) = 1
(17·13)^(2x-2) = (17·13)^0
2x - 2 = 0
2х = 2
х = 1
3) Вычислить значение выражения: 8^log8 6 + 625^log25 sqrt(13)
8^log₈ 6 + 625^log₂₅ √13 = 6 + 25^2log₂₅√13 = 6 + 25^log₂₅13 = 6 + 13 = 19
1) y' = y³x
Проинтегрируем обе части:
Из начального условия y(1)=1 найдем частное решение:
Подставив в общее решение, найдем С
-1/2 = 1/2 + С ⇔ С = -1/4
2)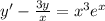
Для начала найдем общее решение однородного дифф. уравнения
Проинтегрировав, получим:
ln|y|=3ln|x| + lnC
y = Cx³ - общее решение однородного дифф. уравнения
y = C(x)x³ подставим в наше дифф. уравнение
Из начального условия y(1) = e найдем C₁
C₁ = 0
1) Найти наибольшее значение функции
y = 1 - log₉ 3^(-x) на отрезке [-1; 5]
Преобразуем функцию
y = 1 - 0,5log₃ 3^(-x)
y = 1 + 0,5х·log₃ 3
y = 1 + 0,5х
находим производную:
y' = 0,5
Производна всегда больше нуля, следовательно, функция у возрастает.
Наибольшее значение находится на правом краю интервала [-1; 5], т.к при х = 5.
у наиб = у(5) = y = 1 + 0,5·5 = 3,5
2) Решить уравнение: 13^(5x-1) · 17^(2x-2) = 13^(3x+1).
17^(2x-2) = 13^(3x+1): 13^(5x-1)
17^(2x-2) = 13^(-2x+2)
17^(2x-2) = 1/13^(2x-2)
(17·13)^(2x-2) = 1
(17·13)^(2x-2) = (17·13)^0
2x - 2 = 0
2х = 2
х = 1
3) Вычислить значение выражения: 8^log8 6 + 625^log25 sqrt(13)
8^log₈ 6 + 625^log₂₅ √13 = 6 + 25^2log₂₅√13 = 6 + 25^log₂₅13 = 6 + 13 = 19