Разложите на множители с-9 где с больше или равно нулю
10-u где u больше или равно нулю
у-d где d и у больше или равно нулю
49w-81d где w и d больше нуля

Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:

Сумма корней приведённого квадратного уравнения x2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.

То есть, если имеется приведённое квадратное уравнение x2 + bx + c = 0, а его корнями являются числа x1 и x2, то справедливы следующие два равенства:

Знак системы (фигурная скобка) говорит о том, что значения x1 и x2 удовлетворяют обоим равенствам.

Объяснение:

62. 7см, 14см, 10см

67. 7  девочек - в тренажерный зал

12 девочек - на шейпинг

14 девочек -на аквааэробику

69.

15 км/ч и 12 км/ч

62. Пусть х- меньшая сторона треугольника, тогда 2х- вторая сторона треугольника и (х+3)- третья сторона треугольника

х+2х+х+3=31 ;

4х=31-3;

х=28:4;

х=7( см)- 1 сторона

2х=2*7=14(см)- вторая сторона

х+3=7+3=10(см) - третья сторона

67.

Пусть в тренаженый зал ходит х старшекласниц, тогда (х+5) старшекласниц ходят на шейпинг и 2х- на аквааэробику.

По условию задачи составим уравнение:

х+х+5+2х=33;

4х=33-5;

х=28:4;

х=7 (ст.) - в тренажерный зал

х+5=7+5=12 (ст.) - на шейпинг

2*7=14 ( ст.) -на аквааэробику

69. Пусть х - скорость второго велосипедиста, а (х+3) - скорость первого. Тогда (х+х+3)- совместная скорость, с которой оба проехали путь до встречи за 40 минут

40минут=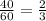 часа

18=(х+х+3)*2/3;

2х+3=18*3/2;

2х=27-3;

х=24:2;

х=12 (км/ч)- скорость второго велосипедиста

х+3=12+3=15(км/ч)- скорость первого велосипедиста