Расстояние между двумя по реке 80 км. пароход совершает этот путь в два конца за 8 ч 20 мин. определить скорость парохода в стоячей воде, считая скорость течения реки 4 км/ч.
Объяснение: Пусть км/ч собственная скорость парохода (скорость парохода в стоячей воде), тогда скорость парохода по течению реки км/ч, с против течения км/ч. Время, которое пароход затрачивает на путь между городами, по течению реки часов, а время против течения часов. По условию путь в оба конца за 8 ч 20 мин ( часа). Составим уравнение:
(км/ч) не подходит, т.к. скорость не может быть отрицательной.
20 км/ч
Объяснение:
8 часов 20 минут = 8 1/3 = 25/3 часа.
Скорость прохода обозначим х, тогда скорость по течению х+4 км/ч, а скорость против течения х-4 км/ч.
80/(x+4) + 80/(x-4) = 25/3
Умножаем все на 3(x-4)(x+4)
240(x-4) + 240(x+4) = 25(x-4)(x+4)
240x - 240*4 + 240x + 240*4 = 25(x^2-16)
480x = 25x^2 - 400
Делим все на 5
5x^2 - 96x - 80 = 0
D = 96^2 + 4*5*80 = 9216 + 1600 = 10816 = 104^2
x1 = (96 - 104)/10 = - 8/10 < 0 - не подходит.
x2 = (96 + 104)/10 = 200/10 = 20 - подходит.
ответ: 20 км/ч.
Объяснение: Пусть км/ч собственная скорость парохода (скорость парохода в стоячей воде), тогда скорость парохода по течению реки
км/ч собственная скорость парохода (скорость парохода в стоячей воде), тогда скорость парохода по течению реки 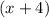 км/ч, с против течения
км/ч, с против течения  км/ч. Время, которое пароход затрачивает на путь между городами, по течению реки
км/ч. Время, которое пароход затрачивает на путь между городами, по течению реки 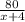 часов, а время против течения
часов, а время против течения 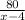 часов. По условию путь в оба конца за 8 ч 20 мин (
часов. По условию путь в оба конца за 8 ч 20 мин (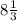
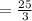 часа). Составим уравнение:
часа). Составим уравнение: