где S - наращенная сумма (сумма которую получит клиент через n лет), P - сумма вклада, i - процентная ставка(годовых), n - срок.
Клиент А положил в банк 3800 рублей, тогда через год он получит рублей. В тех же условиях через год клиент Б получит рублей, в это же время два года для клиента А, он должен получить рублей. Зная, что клиент А получил на 418 рублей больше клиента Б, составим уравнение:
Решаем как квадратное уравнение относительно (1+i)
i₁ < 0 т.е. оно не удовлетворяет условию;
Т.е. под 10% годовых начислял банк по этим вкладам.
Пусть скорость первого поезда x км в час тогда второго y км в час общий путь 5x+3y=500 так как оба числа делятся на два получается 50x+30y=500 10(5x+3y)=500 5x+3y=500 (1) x-y=10 ( или 30 или 20). (2) так как числа должны делиться на 10 ,то подходят только числа 10, 20, 30 если в варианте x-y=10 получается отрицательный ответ y-x=10 решаемых систему 1 и 2 и проверяемых все три варианта 5x+3y=500 3x-3y=30 8x=530 не подходит 8x=590 не подходит 8x=560 подходит x=70 подставляем в исходное уравнение получаем y=50 скорость первого 70 км в ч скорость второго 50 км в ч.
Формула сложной процентной ставки: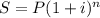
где S - наращенная сумма (сумма которую получит клиент через n лет), P - сумма вклада, i - процентная ставка(годовых), n - срок.
Клиент А положил в банк 3800 рублей, тогда через год он получит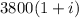
рублей. В тех же условиях через год клиент Б получит 
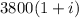рублей, в это же время два года для клиента А, он должен получить 
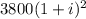рублей. Зная, что клиент А получил на 418 рублей больше клиента Б, составим уравнение:
Решаем как квадратное уравнение относительно (1+i)
i₁ < 0 т.е. оно не удовлетворяет условию;
Т.е. под 10% годовых начислял банк по этим вкладам.
ответ: 10 %.