Пусть х км/ч - скорость течения реки, тогда (18 + х) км/ч - скорость катера, идущего по течению реки, (16 - х) км/ч - скорость катера, идущего против течения реки. Катер, идущий по течению до встречи (18 + х) · 1,5 км, а катер, идущий против течения до встречи (16 - х) · 0,5 км. Так как по условию задачи расстояние между пристанями 37 км и катера встретились, то вместе они расстояние (18 + х) · 1,5 + (16 - х) · 0,5 км, что составляет 37 км. Решим уравнение:
Пусть х км/ч - скорость течения реки, тогда (18 + х) км/ч - скорость катера, идущего по течению реки, (16 - х) км/ч - скорость катера, идущего против течения реки. Катер, идущий по течению до встречи (18 + х) · 1,5 км, а катер, идущий против течения до встречи (16 - х) · 0,5 км. Так как по условию задачи расстояние между пристанями 37 км и катера встретились, то вместе они расстояние (18 + х) · 1,5 + (16 - х) · 0,5 км, что составляет 37 км. Решим уравнение:
(18 + х) · 1,5 + (16 - х) · 0,5 = 37
27 + 1,5х + 8 - 0,5х = 37
1,5х - 0,5х = 37 - 27 - 8
х = 2
ответ: 2 км/ч.
Завдання 1:
Координати точки, яка належить графіку функції (або через яку проходить графік), будуть задовільняти формулу, якою ця функція задана.
Підставимо координати точки В (-2; у) у формулу: абсцису замість х, ординату замість у.
у = -3 ∙ (-2).
Тепер можемо обчислити ординату:
у = 6.
Відповідь: 6.
Завдання 2:
Підставимо координати точки N (-4; 9) у формулу: : абсцису замість х, ординату замість у.
a = 3.
Відповідь: 3.
Завдання 3:
Щоб вирішити рівняння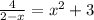
графічно, треба побудувати графіки двох функцій:
Коренями рівняння будуть абсциси точок перетину цих графіків.
Побудуємо графіки, створивши таблицю точок, що належать їм (див. малюнок).
Точка перетину графіків А (1;4).
х = 1.
Відповідь: 1.