При каких значениях а система уравнений: 4х – 7у = а4х -7у =5 имеет бесконечно много решений.

Показать ответ

Ответ:

Tolganay11

18.09.2020 05:45

$63^{72}; \hspace{2mm} 3^{143}*49^{36}; \hspace{2mm} 3^{143}*7^{71}$

Объяснение:

Для начала представим все многочлены в виде произведений простых чисел.

$3^{143}*49^{36} = 3^{143}*(7^2)^{36}=3^{143}*7^{36*2}=3^{143}*7^{72}\\63^{72}=(9*7)^{72}=9^{72}*7^{72}=(3^2)^{72}*7^{72}=3^{72*2}*7^{72}=3^{144}*7^{72}$

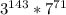А $3^{143}*7^{71}$ так и останется.

Заметим, что у всех трёх произведений одинаковые основания у множетелей: 3 и 7. Это даёт нам возможность сравнивать показатели степеней множителей.

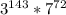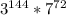Сравним $3^{143}*7^{72}$ и $3^{144}*7^{72}$ . Показатели степени 7 у обоих произведений одинаковы, а вот степень тройки справа на один больше, чем слева. Поэтому правое выражение больше левого.

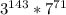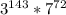Сравним $3^{143}*7^{71}$ и $3^{143}*7^{72}$ . Показатели степени 3 у обоих произведений одинаковы, а вот степень семёрки справа на один больше, чем слева. Поэтому правое выражение больше левого.

Получаем следующий порядок:

$3^{144}*7^{72} 3^{143}*7^{72}3^{143}*7^{71}$

0,0(0 оценок)

Ответ:

2006zahar2006

17.02.2020 02:39

4х²=2х-3
4х²-2х+3=0
D=(-2)²-4×4×3=4-48=-44 D<0, уравнение не имеет корней
----------------------------------------------------------------------------
5х²+26х=24
5х²+26х-24=0
D=26²-4×5×(-24)=676+480=1156 D>0
х₁= $\frac{-26+ \sqrt{1156} }{2*5}= \frac{-26+34}{10} = \frac{8}{10}=0,8$
х₂= $\frac{-26- \sqrt{1156} }{2*5}= \frac{-26-34}{10}= \frac{-60}{10}=-6$
х₁=0,8
х₂=-6
-------------------------------------------------------------------------
3х²-5х=0
D=5²-4×3×0=25-0=25 D>0
х₁= $\frac{-(-5)+ \sqrt{25} }{2*3}= \frac{5+5}{6}= \frac{10}{6}=1,667$
х₂= $\frac{-(-5)- \sqrt{25} }{2*3}= \frac{5-5}{6} \frac{0}{6}=0$
х₁=1,667
х₂=0
--------------------------------------------------------------------
6-2х²=0
-2х²+6=0
D=0²-4×(-2)×6=0+48=48 D>0
х₁= $\frac{-0+ \sqrt{48} }{2*(-2)} = \frac{-0+6,928}{-4}=-1,732
$
х₂= $\frac{-0- \sqrt{48} }{2*(-2)}= \frac{-0-6,928}{-4}= \frac{-6,928}{-4}=1,732$
х₁=-1,732
х₂=1,732
------------------------------------------------------------------
t²=35-2t
t²+2t-35=0
D=2²-4×1×(-35)=4+140=144
t₁= $\frac{-2+ \sqrt{144} }{2*1}= \frac{-2+12}{2}= \frac{10}{2}=5$
t₂= $\frac{-2- \sqrt{144} }{2*1}= \frac{-2-12}{2}= \frac{-14}{2}=-7$
t₁=5
t₂=-7

0,0(0 оценок)

Популярные вопросы: Алгебра