Из этого следует, что уравнение всегда имеет хотя бы одно решение - . Задача сводится к тому, чтобы посмотреть, при каких будут корни у уравнения и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
1) проверим, при каком значении корнем уравнения будет . Подставляем ноль в уравнение: . При имеем:
Делаем вывод, что при уравнение имеет два корня: .
2) при уравнение не может иметь корень . Уравнение - квадратное. Сразу ищем дискриминант:
Здесь рассматриваем 3 случая:
2.1. Если , то уравнение решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
2.2. Если , то подставляя вместо параметра -9 в итоге получаем: . Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
2.3. Если , то уравнение имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит , а мы его проверяли отдельно - при корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
ОТВЕТ: При уравнение имеет единственный корень; при и уравнение имеет два различных корня; при уравнение имеет три различных корня.
1. Функция задана формулой y = −3x + 1. Определите:
1) значение функции, если значение аргумента равно 4;
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=4
у= -3*4+1= -11 при х=4 у= -11
2) значение аргумента, при котором значение функции равно −5;
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -5
-5= -3х+1
3х=1+5
3х=6
х=2 у= -5 при х=2
3) проходит ли график функции через точку A (−2; 7).
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
A (−2; 7)
y = −3x + 1
7= -3*(-2)+1
7=6+1
7=7, проходит.
2. Постройте график функции y = 2x − 5.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = 2x − 5
Таблица:
х -1 0 1
у -7 -5 -3
Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно 3;
Согласно графика, при х=3 у=1
2) значение аргумента, при котором значение функции равно −1.
Согласно графика у= -1 при х=2
3. Не выполняя построения, найдите координаты точек пересечения
графика функции y = −0,6x + 3 с осями координат.
а)График пересекает ось Оу при х=0:
х=0
у= -6*0+3=3
Координаты точки пересечения графиком оси Оу (0; 3)
б)График пересекает ось Ох при у=0.
у=0
0= -0,6х+3
0,6х=3
х=5
Координаты точки пересечения графиком оси Ох (5; 0).
4. При каком значении k график функции y = kx+ 5 проходит через точку
D (6; −19)?
Подставляем известные значения х и у (координаты точки D) в уравнение и вычисляем k:
Перенесем все влево и вынесем за скобки :
:
Из этого следует, что уравнение всегда имеет хотя бы одно решение -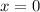 . Задача сводится к тому, чтобы посмотреть, при каких
. Задача сводится к тому, чтобы посмотреть, при каких  будут корни у уравнения
будут корни у уравнения 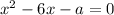 и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
1) проверим, при каком значении корнем уравнения
корнем уравнения 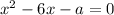 будет
будет 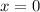 . Подставляем ноль в уравнение:
. Подставляем ноль в уравнение: 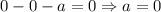 . При
. При 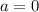 имеем:
имеем:
Делаем вывод, что при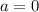 уравнение имеет два корня:
уравнение имеет два корня: 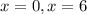 .
.
2) при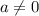 уравнение
уравнение 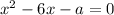 не может иметь корень
не может иметь корень 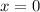 . Уравнение - квадратное. Сразу ищем дискриминант:
. Уравнение - квадратное. Сразу ищем дискриминант: 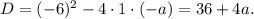
Здесь рассматриваем 3 случая:
2.1. Если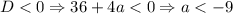 , то уравнение
, то уравнение 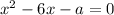 решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
2.2. Если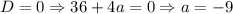 , то подставляя вместо параметра -9 в итоге получаем:
, то подставляя вместо параметра -9 в итоге получаем: 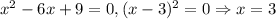 . Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
. Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
2.3. Если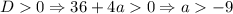 , то уравнение
, то уравнение 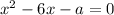 имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит
имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит 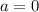 , а мы его проверяли отдельно - при
, а мы его проверяли отдельно - при 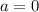 корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
ОТВЕТ: При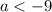 уравнение имеет единственный корень; при
уравнение имеет единственный корень; при 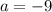 и
и 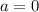 уравнение имеет два различных корня; при
уравнение имеет два различных корня; при 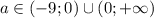 уравнение имеет три различных корня.
уравнение имеет три различных корня.
В решении.
Объяснение:
1. Функция задана формулой y = −3x + 1. Определите:
1) значение функции, если значение аргумента равно 4;
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=4
у= -3*4+1= -11 при х=4 у= -11
2) значение аргумента, при котором значение функции равно −5;
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -5
-5= -3х+1
3х=1+5
3х=6
х=2 у= -5 при х=2
3) проходит ли график функции через точку A (−2; 7).
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
A (−2; 7)
y = −3x + 1
7= -3*(-2)+1
7=6+1
7=7, проходит.
2. Постройте график функции y = 2x − 5.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = 2x − 5
Таблица:
х -1 0 1
у -7 -5 -3
Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно 3;
Согласно графика, при х=3 у=1
2) значение аргумента, при котором значение функции равно −1.
Согласно графика у= -1 при х=2
3. Не выполняя построения, найдите координаты точек пересечения
графика функции y = −0,6x + 3 с осями координат.
а)График пересекает ось Оу при х=0:
х=0
у= -6*0+3=3
Координаты точки пересечения графиком оси Оу (0; 3)
б)График пересекает ось Ох при у=0.
у=0
0= -0,6х+3
0,6х=3
х=5
Координаты точки пересечения графиком оси Ох (5; 0).
4. При каком значении k график функции y = kx+ 5 проходит через точку
D (6; −19)?
Подставляем известные значения х и у (координаты точки D) в уравнение и вычисляем k:
y = kx+ 5
-19=k*6+5
-6k=5+19
-6k=24
k= -4