Задача проще, чем кажется:) Сначала надо представить график функции у = -x^3+3x+2 - это кубическая парабола. у = а - горизонтальная прямая. прямая пересекает параболу - количество точек пересечения может быть такое: 1, 2 или 3. Две точки пересечения - значит, что у исходного уравнения тоже два решения. Две точки пересечения могут быть только в тех точках, где производная равна нулю.: у = -x^3+3x+2 y' = -3x^2+3 y' = 0 при х = 1 и х = -1 (это точки экстремума, видно на графике) а = у(х) = у(-1) = 0 а = у(х) = у(1) = 4
у = -x^3+3x+2 - это кубическая парабола. у = а - горизонтальная прямая.
прямая пересекает параболу - количество точек пересечения может быть такое: 1, 2 или 3. Две точки пересечения - значит, что у исходного уравнения тоже два решения. Две точки пересечения могут быть только в тех точках, где производная равна нулю.:
у = -x^3+3x+2
y' = -3x^2+3
y' = 0 при х = 1 и х = -1 (это точки экстремума, видно на графике)
а = у(х) = у(-1) = 0
а = у(х) = у(1) = 4
ответ: а = 0 и а = 4.
Пусть скорость до увеличения была х км/ч, тогда после увеличения стала (x+10) км/ч. Время пути поезда до увеличения скорости: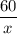 ч.
ч.
Время пути поезда после увеличения скорости: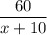 ч.
ч.
Известно, что поезд был задержан на станции на 12 мин = 12/60 ч = 1/5 ч
Составим уравнение:
По т. Виета
50 + 10 = 60 км/ч — скорость поезда после увеличения скорости(или новая скорость).
ответ: первоначальная скорость поезда равна 50 км/ч, а после новая скорость — 60 км/ч.