v1 * t1 = 80, где v - скорость первого работника, t - время его работы,
(v1-1) * (t1+2) = 90, где v1-1 = v2 - скорость второго работника, t1+2 = t2 - его время работы. Выразим t1 из первого уравнения и подставим во второе, раскроем скобки, получим следующее выражение:
v1^2 - 6*v1 - 40 = 0.
В ходе решения системы получаем два корня v:
v1 = 10, v2 = -4.
скорость отрицателньой в данном случае быть не может, поэтому рассматриваем лишь положительный корень. Скорость второго работника на единицу меньше, чем у первого, таким образом,
Из условий задачи формируем систему уравнений:
v1 * t1 = 80, где v - скорость первого работника, t - время его работы,
(v1-1) * (t1+2) = 90, где v1-1 = v2 - скорость второго работника, t1+2 = t2 - его время работы. Выразим t1 из первого уравнения и подставим во второе, раскроем скобки, получим следующее выражение:
v1^2 - 6*v1 - 40 = 0.
В ходе решения системы получаем два корня v:
v1 = 10, v2 = -4.
скорость отрицателньой в данном случае быть не может, поэтому рассматриваем лишь положительный корень. Скорость второго работника на единицу меньше, чем у первого, таким образом,
v2 = 9.
х мальчиков в классе
у девочек в классе
3х/5 мальчиков изучают английский язык
3у/7 девочек изучают английский язык
2х/5 мальчиков изучают немецкий язык
4у/7 девочек изучают немецкий язык
По условию
(3х/5 + 3у/7) > (2х/5 + 4у/7) на 2
Получаем уравнение:
По условию
25 < (x+y) < 36 => (x+y) ∈ (25; 36)
Далее решаем методом подбора.
1) Пусть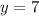
, тогда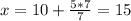 
х=15; у=7
(х+у) = 7+15=22 ∉ (25; 36)
2) Пусть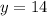
, тогда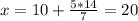 
х=20; у=14
(х+у) = 14+20=34 ∈ (25; 36)
Получаем:
20 мальчиков в классе
14 девочек в классе
20-14 = 6
В классе на 6 мальчиков больше, чем девочек.
ответ под буквой А. Мальчиков, на 6.