Покажите штриховкой на координатной прямой объединение - вопрос №1244137 от татар13 18.05.2022 22:22

Question

Алгебра: Покажите штриховкой на координатной прямой объединение промежутков 1)(-4; 0) и (-1; 5); 2)(-3; 3) и (-6; 6); 3)(-∞; 5) и (-∞; 10)upd: вот ответы

татар13 · Answer

Формула сложной процентной ставки: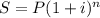 S=P(1+i)^n

где S - наращенная сумма (сумма которую получит клиент через n лет), P - сумма вклада, i - процентная ставка(годовых), n - срок.

Клиент А положил в банк 3800 рублей, тогда через год он получит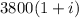 3800(1+i) рублей. В тех же условиях через год клиент Б получит 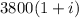рублей, в это же время два года для клиента А, он должен получить 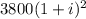3800(1+i)^2 рублей. Зная, что клиент А получил на 418 рублей больше клиента Б, составим уравнение:

$3800(1+i)^2=3800(1+i)+418\\ \\ 3800(1+i)^2-3800(1+i)-418=0~~~|:38\\ \\ 100(1+i)^2-100(1+i)-11=0$

Решаем как квадратное уравнение относительно (1+i)

$D=(-100)^2-4\cdot 100\cdot (-11)=14400$

$(1+i)=\dfrac{-b-\sqrt{D}}{2a}=\dfrac{100-120}{2\cdot100}=-\dfrac{1}{10}~~~\Rightarrow~~~ i_1=-\dfrac{11}{10}$

i₁ < 0 т.е. оно не удовлетворяет условию;

$(1+i)=\dfrac{-b+\sqrt{D}}{2a}=\dfrac{100+120}{2\cdot100}=\dfrac{11}{10}~~~\Rightarrow~~~ i_2=\dfrac{1}{10}=0.1$

Т.е. под 10% годовых начислял банк по этим вкладам.

ответ: 10 %.