Пассажирский поезд должен пройти с постоянной скоростью расстояние между станциями, равное 312 км. когда он половину расстояния, то был задержан на светофоре на 12 минут, поэтому, чтобы наверстать опоздание машинист увеличил скорость поезда на оставшемся участке пути на 5 км в час. с какой скоростью поезд шел после остановки? ( нужно решить по теореме виета)
ответ: 65 км/ч
Объяснение:
1) 312 : 2 = 156 (км) - половина расстояния
2) 12 мин = 12/60 ч = 1/5 ч
Скорость Время Расстояние
До остановки x - 5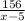 156
156
После ост. x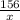 156
156
Время до остановки на 12 мин больше времени после остановки:
х > 5 по смыслу задачи, поэтому умножим обе части уравнения на
5x(x - 5):
780x - 780(x - 5) = x(x - 5)
780x - 780x + 3900 = x² - 5x
x² - 5x - 3900 = 0
По теореме Виета:
x₁ · x₂ = - 3900
x₁ + x₂ = 5
Значит, x₁ = - 60 - не подходит по смыслу задачи
x₂ = 65
ответ: 65 км/ч