Определите значение параметра b, при котором заданное - вопрос №15761592 от warfacegamer01 27.04.2020 19:23

Question

Алгебра: Определите значение параметра b, при котором заданное уравнение не имеет корней. Решение поясните. 2bx + b2 = 2x − 0,5b

warfacegamer01 · Answer

Возведём в квадрат сумму или разность двучлена:

$(x\pm \frac{p}{2})^2=x^2\pm 2\cdot \frac{p}{2}\cdot x+(\frac{p}{2})^2=x^2\pm px+(\frac{p}{2})^2\; \; \; \Rightarrow \\\\\\\boxed {x^2\pm px+q=(x\pm \frac{p}{2})^2-(\frac{p}{2})^2+q}$

Легко запомнить. Чтобы выделить полный квадрат (квадрат двучлена) из квадратного трёхчлена, надо разделить пополам коэффициент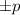 $\pm p$ перед "х" и записать это число в скобку, которая будет возведена в квадрат ( 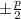$\pm \frac{p}{2}$ ), а затем вычесть квадрат этой половины, а далее приписать свободный член q. Это правило годиться, если коэффициент при 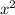x^2 равен 1. Если этот коэффициент не равен 1, то предварительно вынести его за скобку и выделять полный квадрат из выражения, записанного в скобке.

Например:

$x^2-3x+5=(x-\frac{3}{2})^2-\frac{9}{4}+5=(x-1,5)^2+\frac{11}{4}=(x-1,5)^2+2,75$