Чтобы решить квадратное неравенство, следуйте следующему алгоритму...
Нам дано неравенство:
1) Записываем в виде функции:
2) Ищем нули функции (то есть те точки на оси х, в которых парабола пересекает её). Для этого приравниваем трёхчлен к нулю.
Решаем квадратное уравнение:
3) Получившиеся "иксы" - это точки, в которых парабола заныривает под ось Ох. Нам нужно найти промежуток, на котором парабола находится над осью (тк знак ) - смотрите прикреплённый мной рисунок. Парабола имеет положительный коэф-нт k, поэтому ветви вверх. Эту параболу вы должны представить у себя в голове и понять, на каких промежутках ветки находятся в плюсе. То есть над осью х. Это промежутки (-Б;3] и [4;+Б). На промежутке от трёх до четырёх: (3;4) парабола ныряет под ось. То есть там , а нам нужно . Поэтому ответ на чертеже 2.
х=8,5
у=0,5
Пересечение в точке: (8,5;0,5)
Объяснение:
Система:
х²-у²=72 х²-у²=72 х²-(9-х)²=72 х²-(81-18х+х²)=72 ⇒
х+у=9 у=9-х у=9-х у=9-х
⇒ х²-81+18х-х²=72 -81+18х=72 18х=72+81 18х=153 ⇒
у=9-х у=9-х у=9-х у=9-х
⇒ х=153:18 х=8,5 х=8,5 х=8,5
у=9-х у=9-х у=9-8,5 у=0,5
Пересечение в точке: (8,5;0,5)
Чтобы решить квадратное неравенство, следуйте следующему алгоритму...
Нам дано неравенство: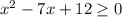
1) Записываем в виде функции: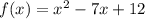
2) Ищем нули функции (то есть те точки на оси х, в которых парабола пересекает её). Для этого приравниваем трёхчлен к нулю.
Решаем квадратное уравнение:
3) Получившиеся "иксы" - это точки, в которых парабола заныривает под ось Ох. Нам нужно найти промежуток, на котором парабола находится над осью (тк знак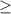
) - смотрите прикреплённый мной рисунок. Парабола имеет положительный коэф-нт k, поэтому ветви вверх. Эту параболу вы должны представить у себя в голове и понять, на каких промежутках ветки находятся в плюсе. То есть над осью х. Это промежутки (-Б;3] и [4;+Б). На промежутке от трёх до четырёх: (3;4) парабола ныряет под ось. То есть там 
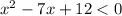, а нам нужно 
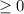. Поэтому ответ на чертеже 2.