Понятно, что это квадратное уравнение. А когда квадратное уравнение будет иметь 2 различных отрицательных корня? Правильно, когда >-b, в данном случае b-коэффициент перед x.
Приступаем к решениею, приведем уравнение к приведенному(разделим на 2)
x^2+1,5x+0,5a=0
Найдём дискриминант
Т.к. в нашем уравнени b-отрицательное число (-1,5), то корню из дискриминанта достаточно принимать значения на промежутке
Потому что, если корень из дискриминанта будет больше 1,5 , то корни получатся либо положительными, либо равными нулю, а этого нам не надо.
Возведем обе части в квадрат, чтобы избавиться от корня
2,25-2a<2,25
-2a<0
a>0
Значит, мы получим 2 различных отрицательных корня, если a>0.
Понятно, что это квадратное уравнение. А когда квадратное уравнение будет иметь 2 различных отрицательных корня? Правильно, когда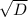 >-b, в данном случае b-коэффициент перед x.
>-b, в данном случае b-коэффициент перед x.
Приступаем к решениею, приведем уравнение к приведенному(разделим на 2)
x^2+1,5x+0,5a=0
Найдём дискриминант
Т.к. в нашем уравнени b-отрицательное число (-1,5), то корню из дискриминанта достаточно принимать значения на промежутке
Потому что, если корень из дискриминанта будет больше 1,5 , то корни получатся либо положительными, либо равными нулю, а этого нам не надо.
Возведем обе части в квадрат, чтобы избавиться от корня
2,25-2a<2,25
-2a<0
a>0
Значит, мы получим 2 различных отрицательных корня, если a>0.