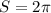Левая часть уравнения не больше (поскольку арксинус принимает значения в промежутке ), правая часть уравнения не меньше (поскольку равна сумме числа и квадрата, который, как известно, не бывает отрицательным). Поэтому обе части должны быть равны Откуда Подставляя полученное значение неизвестной в левую часть уравнения, убеждаемся, что и она в этой точке равна требуемому значению:
Левая часть уравнения не больше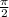 (поскольку арксинус принимает значения в промежутке
(поскольку арксинус принимает значения в промежутке ![\left[-\frac{\pi}{2};\frac{\pi}{2}\right]](/tpl/images/3210/9529/3b5e1.png) ), правая часть уравнения не меньше
), правая часть уравнения не меньше 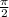 (поскольку равна сумме числа
(поскольку равна сумме числа 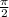 и квадрата, который, как известно, не бывает отрицательным). Поэтому обе части должны быть равны
и квадрата, который, как известно, не бывает отрицательным). Поэтому обе части должны быть равны 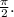 Откуда
Откуда 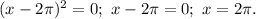 Подставляя полученное значение неизвестной в левую часть уравнения, убеждаемся, что и она в этой точке равна требуемому значению:
Подставляя полученное значение неизвестной в левую часть уравнения, убеждаемся, что и она в этой точке равна требуемому значению: 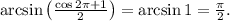
ответ: