Ветви идут вверх, график парабола.
Для того, что бы имелись точки пересечения достаточно, что бы
Что-то никак не могу понять, откуда у меня брались странные символы, но не суть.
данная парабола будет иметь с осью абцисс одну (или несколько) общих точек, если значение у для вершины данной параболы будет:
у = 0(тогда это будет только одна общая точка с осью абцисс)
или у < 0 (тогда это будет две общие точки с осью абцисс)
а для нахождения координат вершины параболы существует формула:
y=ax^2+bx+c
у = -D/4a (по условию а = 1) значит для выполнения задания нам надо что б значение D было больше либо равно нулю
y=x^2+ax+9
D = a^2 - 4*9 >=0
a^2 - 36 >=0
a^2 >= 36
a1 = -6 a2 = 6
порабола y=x^2+ax+9 имеет с осью абцисс одну (или несколько) общих точек при
а принадлежащем (-бесконечности; -6] U [6; + бесконечности)
Ветви идут вверх, график парабола.
Для того, что бы имелись точки пересечения достаточно, что бы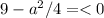
Что-то никак не могу понять, откуда у меня брались странные символы, но не суть.
данная парабола будет иметь с осью абцисс одну (или несколько) общих точек, если значение у для вершины данной параболы будет:
у = 0(тогда это будет только одна общая точка с осью абцисс)
или у < 0 (тогда это будет две общие точки с осью абцисс)
а для нахождения координат вершины параболы существует формула:
y=ax^2+bx+c
у = -D/4a (по условию а = 1) значит для выполнения задания нам надо что б значение D было больше либо равно нулю
y=x^2+ax+9
D = a^2 - 4*9 >=0
a^2 - 36 >=0
a^2 >= 36
a1 = -6 a2 = 6
порабола y=x^2+ax+9 имеет с осью абцисс одну (или несколько) общих точек при
а принадлежащем (-бесконечности; -6] U [6; + бесконечности)