||2^x+x-2|-1| > 2^x-x-1 Раскрывать модули будем постепенно, снаружи, как будто снимая листья с кочана капусты))) Помним о важном правиле: |x| =x, если x>=0 |x|=-x, если x<0
Снимаем первый модуль и действуем согласно вышеупомянутому правилу: {|2^x+x-2|-1 >2^x-x-1 {|2^x+x-2|-1> -2^x+x+1 Переносим "-1" из левой части в правую: {|2^x+x-2| > 2^x-x {|2^x+x-2| > -2^x+x+2
2) Снимаем второй модуль и также действуем согласно модульному правилу: {2^x+x-2>2^x-x {2x-2>0 {2^x+x-2>x-2^x {2*2^x-2>0 {2^x+x-2>-2^x+x+2 {2*2^x-4>0 {2^x+x-2>2^x-x-2 {2x>0
{x>1 {x>1 {2^x>1 {x>0 {2^x>2 {x>1 {x>0 {x>0
Решением неравенства является промежуток (1; + беск.)
Раскрывать модули будем постепенно, снаружи, как будто снимая листья с кочана капусты)))
Помним о важном правиле:
|x| =x, если x>=0
|x|=-x, если x<0
Снимаем первый модуль и действуем согласно вышеупомянутому правилу:
{|2^x+x-2|-1 >2^x-x-1
{|2^x+x-2|-1> -2^x+x+1
Переносим "-1" из левой части в правую:
{|2^x+x-2| > 2^x-x
{|2^x+x-2| > -2^x+x+2
2) Снимаем второй модуль и также действуем согласно модульному правилу:
{2^x+x-2>2^x-x {2x-2>0
{2^x+x-2>x-2^x {2*2^x-2>0
{2^x+x-2>-2^x+x+2 {2*2^x-4>0
{2^x+x-2>2^x-x-2 {2x>0
{x>1 {x>1
{2^x>1 {x>0
{2^x>2 {x>1
{x>0 {x>0
Решением неравенства является промежуток (1; + беск.)
S полн. пов =2430
Объяснение:
Sполн. пов=Sбок.пов+2*Sосн
Sбок.пов=Росн*Н, Н - высота призмы
Sосн=S трапеции =(a+b)*h/2, h - высота трапеции
1. ABCD - трапеция
AB=25, BC=16, CD=17, AD=44.
дополнительные построения:
BM_|_AD, CN_|_AD, BC=MN=16
пусть DN=x, тогда
AD=AM+MN+ND
44=AM+16+x,
AM=44-(16+x), AM=28-x
2. рассмотрим прямоугольный треугольник АМВ:
∠M=90°
гипотенуза АВ=25
катет АМ=28-х
катет ВМ найти по теореме Пифагора:
AM²=AB²-BM²
AM²=25²-(28-x)²
AM²=-x²+56x-159
3. рассмотрим прямоугольный треугольник DNC:
гипотенуза CD=17
катет DN=x
катет CN найти по теореме Пифагора:
CN²=CD²-DN²
CN²=17²-x²
4. BM=CN, =>
уравнение: -х²+56x-159=17²-x²
56x=448
x=8
CN²=17²-8², CN=15
5.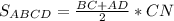
6. S полн. пов=(25+16+17+44)*15+2*450=2430