Войти
Регистрация
Спроси ai-bota
В
Все
Б
Биология
Б
Беларуская мова
У
Українська мова
А
Алгебра
Р
Русский язык
О
ОБЖ
И
История
Ф
Физика
Қ
Қазақ тiлi
О
Окружающий мир
Э
Экономика
Н
Немецкий язык
Х
Химия
П
Право
П
Психология
Д
Другие предметы
Л
Литература
Г
География
Ф
Французский язык
М
Математика
М
Музыка
А
Английский язык
М
МХК
У
Українська література
И
Информатика
О
Обществознание
Г
Геометрия
Показать больше
Показать меньше
Luka2015
19.10.2020 17:08 •
Алгебра
Найти наибольшее и наименьшее значение функции на отрезке
f(x)3x^4-6x^2+3 на отрезке [-2;2]
Показать ответ
Ответ:
kymbatbadagulovа
27.03.2022 08:40
Объяснение:
область определения функции
- симметричное множество
.
, значит, функция четная,
0,0
(0 оценок)
Популярные вопросы: Алгебра
lefuxetube
04.06.2021 17:12
Напишите какую-нибудь арифметическую прогрессию, состоящую из шести членов, каждый из которых представляет собой обыкновенную дробь, причем знаменатели всех дробей различны,...
Vika10023
18.01.2021 02:39
Значение выражения 3+b/24 равно нулю, если b=...
TheVladChannel
27.07.2022 17:56
3.Для острого угла α найдите sin α, , tg α, ctg α, если cos α =0,8...
vladislavaky
28.05.2021 08:31
№1. Выполните действия: а) 27x2y∙34x3∙7y2 ; б) 8xy2z4:1.6y2z. №2. Упростите: (2x3y5)8∙2x3y14(2x3y6)9 .№3.Приведите одночлен к стандартному виду: -52pq7(-24p3q∙p2). №4.Найдите...
vladekan
08.05.2021 11:13
1. Найдите 22-й член арифметической прогрессии (аn), если а1 = 5,8 и d = -1,5. 2. Найдите сумму 9 первых членов арифметической прогрессии (bn): 6,4; 7,2; 8; ... 3. Найдите...
kozlovvlad21
14.10.2020 23:50
У=√3х^2-4х+1 +√х^2-4...
Freidan
16.06.2021 15:53
За якого значення а добуток коренів квадратного рівняння x²+3x+(a²+2a-15)=0 дорівнює нуль?...
osheefit
22.08.2020 16:48
Найди скорость изменения функции в точке x: y=−3x+9...
Vov1111
15.11.2022 04:23
Для вибірки заданої статистичним рядом знайдіть розмах моду середнє значення сукупності значеннь та побудуйте полігон частот х 2 4 5 6 n 8 9 10 3...
popirina2001
07.01.2021 21:26
Постройте график уравнения x + y = -2. При каком значении а пара чисел (-1; 3) является решением уравнения 5x – 3y = a? При каком значении а проходит через начало координат...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Объяснение:
область определения функции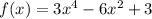 - симметричное множество
- симметричное множество 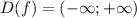 .
. 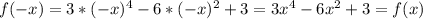 , значит, функция четная,
, значит, функция четная,