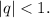Бесконечно убывающая геометрическая прогрессия с первым членом и знаменателем . ВАЖНО: геометрическая прогрессия бесконечно убывающая тогда, когда
Бесконечно убывающая геометрическая прогрессия с первым членом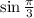 и знаменателем
и знаменателем 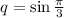 . ВАЖНО: геометрическая прогрессия бесконечно убывающая тогда, когда
. ВАЖНО: геометрическая прогрессия бесконечно убывающая тогда, когда