Найдите площадь фигуры, ограниченной линиями:

у= -4/x; y= 2; x= -2; x= -1

 √(12+x)=1+ √(1-x)

Возводим в квадрат обе части уравнения

12+x=1+2 √(1-x)+(1-x)

12+x-1-1+x=2 √(1-x)

10+2x=2 √(1-x) Делим все на2

5+x= √(1-x)

Опять возводим в квадрат

25+10x+x^2=1-x

x^2+10x+x+25-1=0

x^2+11x+24=0

D=121-4*24

D=25

x1=(-11+5)/2=-3

x2=(-11-5)/2=-8

Делаем обязательно проверку

x1=-3

  √(12-3)- √(1+3)= 1

 √9- √4=3-2=1

1=1. Значит х1=-3 корень

x2=-8 

√(12-8)- √(1+8)= 1

√(4- √(9)= 1. Получаем 2-3=-1

-1не=1. Значит x2=-8 посторонний корень

ответ: x=-3

КейтМиделтон блестяще справилась с подсчетом числа различных выбрать размеры групп, не забыв учесть тот факт, что группы пронумерованы.

А теперь давай решим задачу.

Предположим, что в первой группе k человек, тогла во второй группе будет 12-k человек, где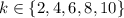 . Давай подумаем, сколько существует различных выбрать k учеников из двенадцати (таблицу составлять не будем). Осуществляется выбор без возвращения и без учета порядка, ответ известен — биномиальный коэффициент .

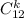Складывая эти числа для всевозможных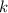 , получаем ответ: