Найдём функцию Эйлера от числа 5. Это количество чисел, меньших 5 и взаимно простых с ним, то есть не имеющих с 5 общих делителей. Такими числами являются 1, 2, 3, 4, поскольку они не делятся на 5. Тогда функция Эйлера φ(5) = 4 (к тому же функция Эйлера простого числа, каким является 5, представляет собой результат вычитания единицы из этого числа, то есть 5 - 1 = 4, как у нас и получилось).
Так как 3 и 5 — взаимно простые числа, то сравнимо с 1 по модулю 5.
2020 = 5 * 404
Тогда можно записать в виде
Поскольку мы выяснили, что сравнимо с 1 по модулю 5, то также сравнимо с 1 по модулю 5. То есть остаток равен 1.
1
Объяснение:
Найдём функцию Эйлера от числа 5. Это количество чисел, меньших 5 и взаимно простых с ним, то есть не имеющих с 5 общих делителей. Такими числами являются 1, 2, 3, 4, поскольку они не делятся на 5. Тогда функция Эйлера φ(5) = 4 (к тому же функция Эйлера простого числа, каким является 5, представляет собой результат вычитания единицы из этого числа, то есть 5 - 1 = 4, как у нас и получилось).
Так как 3 и 5 — взаимно простые числа, то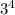 сравнимо с 1 по модулю 5.
сравнимо с 1 по модулю 5.
2020 = 5 * 404
Тогда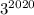 можно записать в виде
можно записать в виде 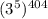
Поскольку мы выяснили, что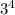 сравнимо с 1 по модулю 5, то
сравнимо с 1 по модулю 5, то 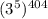 также сравнимо с 1 по модулю 5. То есть остаток равен 1.
также сравнимо с 1 по модулю 5. То есть остаток равен 1.