Перед тем как выражать , нужно рассмотреть случаи, когда дробь положительная, а когда отрицательная:
Если такая дробь положительная, то при нахождении переменной знак неравенства меняться не будет (так как делим (умножаем) на положительное число):
Решим неравенство методом интервалов.
а) ОДЗ:
б) Нуль неравенства:
в) Решением данного неравенства будет .
При таких значениях параметра знак неравенства меняться не будет:
Если такая дробь отрицательная, то при нахождении переменной знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):
Решим неравенство методом интервалов. Решением данного неравенства будет .
При таких значениях параметра знак неравенства изменится:
ответ: если , то ; если , то ; если и , то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра , поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если , то есть , то в объединении с получаем при Если , то есть , то в объединении с получаем, что таких не существует, то есть такого варианта эта система не имеет.
2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:
ответ: если , то ; если , то ; если , то система не имеет решений.
Пусть угол KPD - a, угол MNB - b, а угол MPD - c. a=4(b+c)(по условию), b=c(соответственные углы), a+c=180°(смежные углы). Составляем систему: a+b=180° и a=8b => a+b=180° и a=8b => 8b+b=180° и a=8b => 9b=180° и a=8b => b=20° и a=160° ответ: a=160°, b=20°, c=20°.
Если угол C и угол BDC равны 60°, то и угол DBC равен 60°, следовательно, треугольник BDC - равносторонний, а BC и BD равны 5 см. Если угол BDC равен 60°, а угол ABD равен 30°, то угол ADB равен 120° (как смежный с BDC), а угол BAD равен 30°, следовательно, треугольник ABD - равнобедренный, а AD равно 5 см. AC=5 см + 5 см = 10 см ответ: AC=10 см, AD=5 см.
1. Решим первое неравенство этой системы:
ответ: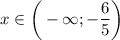
2. Дробь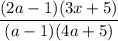 существует, если
существует, если
Перед тем как выражать , нужно рассмотреть случаи, когда дробь
, нужно рассмотреть случаи, когда дробь 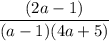 положительная, а когда отрицательная:
положительная, а когда отрицательная:
Если такая дробь положительная, то при нахождении переменнойРешим неравенство методом интервалов.
а) ОДЗ: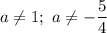
б) Нуль неравенства: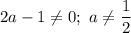
в) Решением данного неравенства будет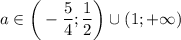 .
.
При таких значениях параметра знак неравенства меняться не будет:
знак неравенства меняться не будет:
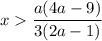
Если такая дробь отрицательная, то при нахождении переменнойРешим неравенство методом интервалов. Решением данного неравенства будет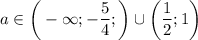 .
.
При таких значениях параметра знак неравенства изменится:
знак неравенства изменится:
ответ: если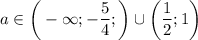 , то
, то 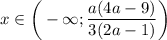 ; если
; если 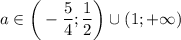 , то
, то 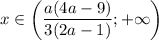 ; если
; если 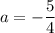 и
и 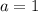 , то неравенство не имеет решений.
, то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра , поэтому:
, поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:ответ: если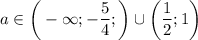 , то
, то 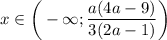 ; если
; если 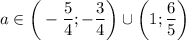 , то
, то 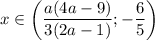 ; если
; если ![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png) , то система не имеет решений.
, то система не имеет решений.
a=4(b+c)(по условию), b=c(соответственные углы), a+c=180°(смежные углы). Составляем систему: a+b=180° и a=8b => a+b=180° и a=8b => 8b+b=180° и a=8b => 9b=180° и a=8b => b=20° и a=160°
ответ: a=160°, b=20°, c=20°.
Если угол C и угол BDC равны 60°, то и угол DBC равен 60°, следовательно, треугольник BDC - равносторонний, а BC и BD равны 5 см. Если угол BDC равен 60°, а угол ABD равен 30°, то угол ADB равен 120° (как смежный с BDC), а угол BAD равен 30°, следовательно, треугольник ABD - равнобедренный, а AD равно 5 см. AC=5 см + 5 см = 10 см
ответ: AC=10 см, AD=5 см.