Здесь нужно найти такое , при котором выполняется .
Составим уравнение и решим его:
Следовательно, мяч побывает на высоте метров ровно раза: через и через секунды после своего отправления.
В).
Раз коэффициент при отрицательный (он равен ), то ветви параболы направлены вниз и максимальное значение функции будет достигаться в вершине параболы, которая имеет абсциссу . Теперь найдем само в этой точке (ординату):
Делаем вывод, что наибольшая высота, которую достиг мяч - это метра.
А).
Через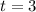
секунды мяч будет на следующей высоте:
Б).
Здесь нужно найти такое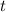
, при котором выполняется 
.
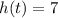Составим уравнение и решим его:
Следовательно, мяч побывает на высоте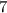
метров ровно 
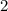раза: через 
и через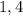 
секунды после своего отправления.
В).
Раз коэффициент при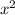
отрицательный (он равен 
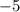), то ветви параболы направлены вниз и максимальное значение функции 
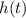будет достигаться в вершине параболы, которая имеет абсциссу 
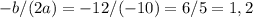. Теперь найдем само 
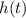в этой точке (ординату):
Делаем вывод, что наибольшая высота, которую достиг мяч - это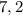
метра.
60 км/час - скорость первого автомобиля
50 км/час - скорость второго автомобиля
Объяснение:
х+10 - скорость первого автомобиля
х - скорость второго автомобиля
300/x+10 - время в пути первого автомобиля
300/х - время в пути второго автомобиля
По условию задачи разница во времени 1 час:
300/x - 300/x+10 = 1 Общий знаменатель х(х+10):
300(х+10) - 300х = х(х+10)
300х+3000-300х=х²+10х
-х²-10х+3000 = 0
х²+10х-3000=0, квадратное уравнение, ищем корни:
х₁,₂ = (-10±√100+12000)/2
х₁,₂ = (-10±√12100)/2
х₁,₂ = (-10±110)/2
х₁ = -60, отбрасываем, как отрицательный
х₂ = 50 (км/час - скорость второго автомобиля)
50+10=60 (км/час - скорость первого автомобиля)
Проверка:
300 : 50 = 6 (часов был в пути второй автомобиль)
300 : 60 = 5 (часов был в пути первый автомобиль)
Разница 1 час, как в условии задачи.