1. Решим квадратное уравнение: . Т. к. дискриминант равен нулю, то корень здесь один: . Парабола касается оси Ox в точке (1;0), а так как коэффициент при иксе в квадрате положительный, значит, ветви параболы направлены вверх. Из этого следует, что y>0 при x∈(-∞; 1)∪(1; +∞), а при x=1 функция равна нулю
2. Область определения функции -- это x∈[0; +∞). Т. к. квадратный корень из числа всегда равен неотрицательному числу, к которому к тому же прибавляется два (в данной функции), то на всей области определения функция положительна: y>0 при x∈[0; +∞).
3. Область определения функции -- это x∈[-2; +∞). Функция равна нулю при x=-2, а на остальной области определения положительна: y>0 при x∈(-2; +∞).
1. Решим квадратное уравнение: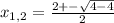
. Т. к. дискриминант равен нулю, то корень здесь один: 
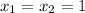. Парабола касается оси Ox в точке (1;0), а так как коэффициент при иксе в квадрате положительный, значит, ветви параболы направлены вверх. Из этого следует, что y>0 при x∈(-∞; 1)∪(1; +∞), а при x=1 функция равна нулю
2. Область определения функции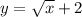
-- это x∈[0; +∞). Т. к. квадратный корень из числа всегда равен неотрицательному числу, к которому к тому же прибавляется два (в данной функции), то на всей области определения функция положительна: y>0 при x∈[0; +∞).
3. Область определения функции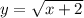
-- это x∈[-2; +∞). Функция равна нулю при x=-2, а на остальной области определения положительна: y>0 при x∈(-2; +∞).
t^4+(t-4)^4=626,
t^4+(t^2-8t+16)^2=626,
t^4+t^4-8t^3+16t^2-8t^3+64t^2-128t+ 16t^2-128t+256=626,
2t^4-16t^3+96t^2-256t+256=626,
Делим на 2 обе части:
t^4-8t^3+48t^2-128t+128=313,
t^4-8t^3+48t^2-128t-185=0,
t^4+t^3-9t^3-9t^2+57t^2+57t-185t-185 =0, t^3(t+1)-9t^2(t+1)+57t(t+1)-185(t+1)=0
(t+1)(t^3-9t^2+57t-185)=0,
(t+1)(t^3-5t^2-4t^2+20t+37t-185)=0,
(t+1)(t^2(t-5)-4t(t-5)+37(t-5))=0,
(t+1)(t-5)(t^2-4t+37)=0,
Найдем корни уравнения
t^2-4t+37=0, t=(4+-√(16-4*37))/2,
16-4*37<0, поэтому вещественных корней нет, тогда получаем
t+1=0, t-5=0, t=-1, t=5,
3x+2=-1, 3x=-3, x=-1
3x+2=5, 3x=3, x=1
ответ: x=-1, x=1.