23.17 p(x)=(2х+1)(4х^2-2х+1)-8х^3=(8х^3-4x^2+2x+4x^2-2x+1)-8x^3=1 То есть при любых значениях х ответ будет всегда 1.
23.18р(х;у)=(ху+3)(2ху-4)-2(ху-7)=2*x^2*y^2-4xy+6xy-12-2xy+14=2*x^2*y^2+2 Разберем по частям 2*x^2*y^2+2 1) 2*x^2*y^2 всегда положителен, так как квадрат числа не может быть отрицательным, положительное число{2}умножаем{x^2}и умножаем на {y^2} = положительное число, всегда положителен 2) число 2>0, положительное число 3) сумма двух положительных чисел {2*x^2*y^2 и 2} всегда дает нам положительное число
p(x)=(2х+1)(4х^2-2х+1)-8х^3=(8х^3-4x^2+2x+4x^2-2x+1)-8x^3=1
То есть при любых значениях х ответ будет всегда 1.
23.18р(х;у)=(ху+3)(2ху-4)-2(ху-7)=2*x^2*y^2-4xy+6xy-12-2xy+14=2*x^2*y^2+2
Разберем по частям 2*x^2*y^2+2
1)
2*x^2*y^2 всегда положителен, так как квадрат числа не может быть отрицательным, положительное число{2}умножаем{x^2}и умножаем на {y^2} = положительное число, всегда положителен
2)
число 2>0, положительное число
3) сумма двух положительных чисел {2*x^2*y^2 и 2} всегда дает нам положительное число
x = 7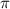
/6
Объяснение:
2 sin x = -1
sin x = -0.5
Отмечаем нужные точки на тригонометрическом круге
Это x = -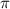
/6 + 2
Так же можно задать это множество решений так:
x =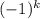
* (-
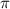/6) +
Нам нужно выбрать из множества решений только те, которые принадлежат заданному промежутку.
Отметим этот промежуток на тригонометрическом круге
Из рисунка видно, что подходит только одно решение x = 7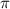
/6
Это решение можно было найти другим решив неравенство
1/2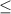
7/6 + 2k
3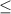
7 + 12k
Так как k - целое, то подходит только k = 0, при других целых k неравенство не выполняется.
1/2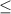
-1/6 + 2k
3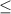
-1 + 12k
Здесь нет целых значений k, для которых бы выполнялось неравенство (при k = 0 -1+0<3, при k = 1 -1+11>9)
Значит, решением является только x = 7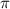
/6
Но здесь проще находить решение именно из тригонометрического круга по рисунку.