Люди ! написал как мог чтобы было вам понятно) здрасьте)люди болел на этой вот прям вот формулы примеры как надо решать,но и то я и их не понял: 1.sin x=0,2 x=arcsin 0,2+2пk, k(принадлежит)z x=п-arcsin0,2+2пk,
k(принадлежит)z к синусу косинусу тангинсу и катангинсу есть свои формулы и к чему то нужно примечать минус или просто пk,но у меня пример формулы только с синусом(вот и надо так же решить примеры,кстати вот и они
внизу) 1)tg(в квадрате) x+tg x=0 2)cos(в квадрате) x =3/4 3)sin(в квадрате) x -4 sin x +3=0 4)cos(3п/4 - 2x) =-1 5)cos3x=-1/2 6)2cos(в квадрате)+3sinx=0 7)sin2x cosx-3sin(в квадрате)x=0 поmотите люди добрые
1) tg² x + tg x = 0,
tg x (tg x + 1) = 0,
tg x = 0 или tg x + 1 = 0, tg x = -1,
x=πk, k∈Z или x=arctg(-1)+πk, k∈Z, x=π-arctg1+πk, k∈Z, x=π-π/4+πk, k∈Z, x=3π/4+πk, k∈Z,
2)cos² x =3/4,
cos x =-√3/2 или cos x =√3/2,
[x=±arccos(-√3/2)+2πk, k∈Z, x=±arccos(√3/2)+2πk, k∈Z,
[x=±(π-arccos(√3/2))+2πk, k∈Z, x=±π/6+2πk, k∈Z,
x=±(π - π/6)+2πk, k∈Z,
x=±5π/6+2πk, k∈Z, или x=±π/6+2πk, k∈Z,
3)sin² x -4 sin x +3=0,
sin x = t,
t^2-4t+3=0,
по теореме обратной к теореме Виета:
t1=1, t2=3>1,
sin x = 1,
x = π/2+2πk, k∈Z,
4)cos(3π/4 - 2x) =-1,
3π/4 - 2x=π+2πk, k∈Z,
-2x=π/4 + 2πk, k∈Z,
x=-π/8 - πk, k∈Z,
5)cos3x=-1/2,
3x=±arccos(-1/2)+2πk, k∈Z,
3x=±(π-arccos(1/2))+2πk, k∈Z,
3x=±(π - π/3)+2πk, k∈Z,
3x=±2π/3+2πk, k∈Z,
x=±2π/9+2π/3 k, k∈Z,
6)2cos² x + 3sin x = 0,
2(1-sin² x) + 3sin x = 0,
-2sin² x + 3sin x + 2 = 0,
2sin² x - 3sin x - 2 = 0,
sin x = t,
2t^2-3t-2=0,
D=25,
t1=-1/2, t2=2>1,
sin x = -1/2,
x=(-1)^k arcsin(-1/2)+πk, k∈Z,
x=(-1)^k (-arcsin (1/2))+πk, k∈Z,
x=(-1)^(k+1) π/6+πk, k∈Z,
7)sin2x cos x - 3sin²x=0,
2sin x cos x cos x - 3sin²x = 0,
2sin x cos² x - 3sin²x = 0,
2sin x (1-sin² x) - 3sin²x = 0,
sin x (2-4sin² x) = 0,
sin x = 0 или 2-4sin² x=0, sin² x=1/2, sin x = -1/√2 или sin x = 1/√2,
x = πk, k∈Z,
или x=(-1)^k arcsin(-1/√2)+πk, k∈Z, x=(-1)^k (-arcsin(1/√2))+πk, k∈Z, x=(-1)^(k+1) π/4+πk, k∈Z,
или x=(-1)^k arcsin(1/√2)+πk, k∈Z, x=(-1)^k π/4+πk, k∈Z
1) Выносим tgx,получаем:tgx(tgx+1)=0.Каждый множитель приравниваем к нулю:tgx=0 и (tgx+1)=0.Решаем по отдельности: tgx=0 ; x=Пk, где k принадлежит Z.(tgx+1)=0;tgx=-1;x=-arctg1+Gk,где k принадлежит Z.
2)Cosx=кв. корень 3.4;извлекаем корень:Cosx=корень из трех деленое на два;x=+- П/6+2Пk,где k принадлежит Z.
3)Вводим новую переменную: Sinx=t,причем t по модулю меньше равняется 1;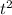 -4t+3=0,решаем дескрименант,он равен 4,ищем корни: t1=1, t2=4.подставляем сюда Sinx=t,получаем:Sinx=1 x=(-1)в степени n * 1 + Пk,где k принадлежит Z; Sinx=4 по аналогии.
-4t+3=0,решаем дескрименант,он равен 4,ищем корни: t1=1, t2=4.подставляем сюда Sinx=t,получаем:Sinx=1 x=(-1)в степени n * 1 + Пk,где k принадлежит Z; Sinx=4 по аналогии.
ост. чуть позже.