В задании немного некорректно написаны корни, поэтому:
Если задание такое , то
перегрупировав слагаемые мы получили линейную функцию, которой максимум 1 корень. Так как в эта функция зависит от х, то 1 решение гарантированно.
Если задание такое , то
Возводив в квадрат мы получим квадратное уравнение, у которого максимум 2 корня. но поскольку везде будут знаки + (мы возведём в квадрат, чтобы избавится от корня), и свободный член не равен 0, то решений нет, так как дискриминант меньше нуля.
Это линейная функция
1) Область определения - множество R
2) Область значений - множество R, если к не равно 0, а если к =0, то число b
3) При к не равно 0, функция ни парная ни непарная; если к =0, то функция парная; если b =0, то функция непарная
4) При к>0 функция возрастает, при к <0 функция убывает, при к =0 постоянная
5) Функция не имеет экстремумов
6) График - прямая, не проходящая через начало координат
7) При b =0 функция имеет вид у = кх. график - прямая, проходящая через начало координат
Объяснение:
В задании немного некорректно написаны корни, поэтому:
Если задание такое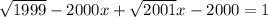 , то
, то
перегрупировав слагаемые мы получили линейную функцию, которой максимум 1 корень. Так как в эта функция зависит от х, то 1 решение гарантированно.
Если задание такое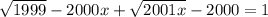 , то
, то
Возводив в квадрат мы получим квадратное уравнение, у которого максимум 2 корня. но поскольку везде будут знаки + (мы возведём в квадрат, чтобы избавится от корня), и свободный член не равен 0, то решений нет, так как дискриминант меньше нуля.