Разобьём отрезок произвольным образом на n частей точками:
В каждом интервале произвольным образом выбираем точку
Cумма
,
где - длина частичного отрезка ,
называется интегральной суммой функции на отрезке .
Определенным интегралом от функции на отрезке называется предел интегральных сумм , при условии, что длина наибольшего частичного отрезка стремится к нулю
Геометрическая интерпретация определённого интеграла - площадь криволинейной трапеции
Для того, чтобы назвать модель математической, необходимо наличие трех вещей:
1) Ввести переменные
2) задать область, на которой будет рассмотрена задача
3) составить функцию цели. т.е. определить, как решать поставленную условием задачу.
Переменные берем из вопроса. Что надо найти? скорость каждого автомобиля. Поэтому введем переменные v₁ и v₂ - скорости первого и второго автомобилей соответственно.
Обе переменные больше нуля.
Расстояние можно найти, если знаем время и скорость. кратко запишем условие с таблицы.
s v t
1 автомобиль 180км ?v₁ 1ч.36мн=1 .6ч/после встречи/
2 автомобиль 180км ?v₂ 2ч 30 мин.=2.5ч/после встречи/
Расстояние Время
До встречи После встречи скорость до после
1 х 180-х v₁ одинак. 1.6
2 180-х х v₂ одинак. 2.5
Пусть первый до встречи проехал х км, тогда второй (180-х) км.
До встречи затратили одно и то же время, т.к. вышли одновременно.
х/v₁=(180-х)/ v₂
v₁1.6+ v₂*2.5=180
Составлена система двух уравнений с двумя переменными. Собственно цель - найти переменные - значения скоростей. После решения системы выполнить отбор полученных решений и записать ответ.
Пусть функция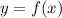 определена на отрезке
определена на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png)
Разобьём отрезок произвольным образом на n частей точками:
В каждом интервале произвольным образом выбираем точку
Cумма
где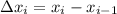 - длина частичного отрезка
- длина частичного отрезка ![[x_{i-1};x_{i}]](/tpl/images/1361/6254/3b10f.png) ,
,
называется интегральной суммой функции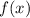 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) .
.
Определенным интегралом от функции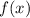 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) называется предел интегральных сумм
называется предел интегральных сумм 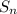 , при условии, что длина наибольшего частичного отрезка стремится к нулю
, при условии, что длина наибольшего частичного отрезка стремится к нулю
Геометрическая интерпретация определённого интеграла - площадь криволинейной трапеции
Для того, чтобы назвать модель математической, необходимо наличие трех вещей:
1) Ввести переменные
2) задать область, на которой будет рассмотрена задача
3) составить функцию цели. т.е. определить, как решать поставленную условием задачу.
Переменные берем из вопроса. Что надо найти? скорость каждого автомобиля. Поэтому введем переменные v₁ и v₂ - скорости первого и второго автомобилей соответственно.
Обе переменные больше нуля.
Расстояние можно найти, если знаем время и скорость. кратко запишем условие с таблицы.
s v t
1 автомобиль 180км ?v₁ 1ч.36мн=1 .6ч/после встречи/
2 автомобиль 180км ?v₂ 2ч 30 мин.=2.5ч/после встречи/
Расстояние Время
До встречи После встречи скорость до после
1 х 180-х v₁ одинак. 1.6
2 180-х х v₂ одинак. 2.5
Пусть первый до встречи проехал х км, тогда второй (180-х) км.
До встречи затратили одно и то же время, т.к. вышли одновременно.
х/v₁=(180-х)/ v₂
v₁1.6+ v₂*2.5=180
Составлена система двух уравнений с двумя переменными. Собственно цель - найти переменные - значения скоростей. После решения системы выполнить отбор полученных решений и записать ответ.