Докажите, что если дробь а-в/а+в, где а и в - некоторые натуральные числа, причем а> в, несократимые числа, то несократима также и дробь а/в.

Доказательство от противного:

Предположим, дробь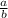 сократима. Это означает, что у чисел а и b есть общий простой множитель (назовем его k). Тогда число а можно представить в виде произведения mk, а число b - в виде произведения nk. Заменим а и b в дроби 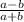на эти выражения, получим:

.

Вынесем k за скобки:

Числитель и знаменатель этой дроби можно сократить на k, но это противоречит условию, в котором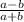 - несократимая дробь. Значит, наше предположение о том, что дробь 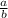сократима - неверно, т.е эта дробь является несократимой (что и требовалось доказать)