y(x) = 3log(x) + C1*x²/2 + C2*x + C3 (C1, C2, C3 - константы)
Объяснение:
x³ * y''' = 6
Запишем это как x³ * * y(x) = 6
* y(x) = 6/x³
Начнем интегрировать.
= ∫ 6/x³ dx = -3/x²+ C1 (C1 - константа)
= ∫ (-3/x² + C1) dx = 3/x + C1x + C2 (C2 - константа)
y(x) = ∫ (3/x + C1x + C2) dx = 3log(x) + C1x²/2 + C2x + C3 (C3 - константа)
см. во вложении
y(x) = 3log(x) + C1*x²/2 + C2*x + C3 (C1, C2, C3 - константы)
Объяснение:
x³ * y''' = 6
Запишем это как x³ *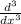 * y(x) = 6
* y(x) = 6
Начнем интегрировать.
y(x) = ∫ (3/x + C1x + C2) dx = 3log(x) + C1x²/2 + C2x + C3 (C3 - константа)
см. во вложении
Объяснение: