Дана функция y=〖(x+2)〗^2-1 а) Определите координаты вершины параболы.
б) Приведите функцию к виду ax^2+bx+c=0
в) В какой точке график данной функции пересекает ось ОY?
г) Найдите точки пересечения графика функции с осью ОХ.
д) Постройте график функции.
сумма n последовательных нечетных натуральных чисел при n>1
1+3+5+7+...+(2n-1)=n^2
Доказательство методом математической индукции
База индукции
n=2. 1+3=2^2
Гипотеза индукции
Пусть для n=k утверждение выполняется, т.е. выполняется
1+3+5+7+...+(2k-1)=k^2
Индукционный переход. Докажем, что тогда выполняется утверждение и для n=k+1, т.е, что выполняется
1+3+5+7+...+(2k-1)+(2K+1)=(k+1)^2
1+3+5+7+...+(2k-1)+(2K+1)=используем гипотезу МИ=k^2+(2k+1)=k^2+2k+1=используем формлу квадрату двучлена=(k+1)^2, что и требовалось доказать.
По методому математической индукции формула справедлива.
Число n^2 при n>1 zвляется составным, оно делится на 1,n,n^2.
А значит сумма n последовательных нечетных натуральных чисел при n>1 является составным числом. Доказано
Покажу один из сопособов решения таких неравенств
1) проверим ограничения
2) введем замену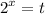
получаем,
А далее самое интересное
будем делить многочлен на многочлен
_t²-16t+30 | t-2 и _t²-7t+3 | t-7
t²-2t ______ t²-7t _____
_____ t-14 ____ t
_ -14t+30 3 (остаток)
-14t+28
------------
2 (остаток)
тогда
теперь все совсем просто
решаем методом интервалов
__-____ 2 ___+____4___-____7___+____
Не забываем проверить ограничение
ответ (-∞; 1)∪[2; log₂7)