Чи правильно, що графік функції у = 2х – 6 перетинає вісь ОУ у точці: 1) з додатною ординатою; 2) з від'ємною ординатою; 3) з ординатою, що дорівнює 0?

Показать ответ

Ответ:

Tasha00000007

23.10.2021 18:45

Объяснение:

Пусть первоначальная стоимость стола - х грн, тогда первоначальная стоимость стула - у грн ,при этом три стола и четыре стула стоили

3х +4у = 3000 разделим обе части на 3

х+4/3у = 1000, отсюда х = 1000-4/3у

После того как уценили стол на 10% стоимость стола стала 100%-10%=90%,то есть 0,9х

а после уценки стула на 20% он стал стоить 100%-20%=80% то есть

0,8у , но так как стульев два штуки то получим 2*0,8у. В результате получим

0,9х +2*0,8у = 960 подставляем в уравнение х, тогда имеем

0,9* (1000-4/3у) + 1,6у = 960

900 - 1,2у +1,6у =960

0,4у =960 -900

0,4у= 60

у= 60: 0,4

у= 150 грн стоимость стула

х= 1000-4/3*150= 1000-200= 800 грн стоимость стола

Проверка: 3* 800 +4* 150= 2400+600= 3000 грн

0,0(0 оценок)

Ответ:

оксаночка1412

21.03.2022 09:35

Из 12 учеников, выбрать ученика, которому мы дадим первую книгу, можно После этого остается 11 учеников без книг. Из них выбрать следующего ученика, которому мы дадим вторую книгу, можно

Общее число раздать разные (!) книги существует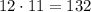 $12\cdot 11=132$ .

Другими словами, мы находили размещение из 12 по 2:

$A_{12}^2=\dfrac{12!}{(12-2)!} =12\cdot11=132$

А вот если книги были бы одинаковыми, то порядок выбора учеников был бы не важен: все выбранные ученики получили бы одинаковые книги. В этом случае мы вычисляем сочетание из 12 по 2:

$C_{12}^2=\dfrac{12!}{(12-2)!\cdot2!} =\dfrac{12\cdot11}{1\cdot2} =66$