Войти Регистрация Спроси ai-bota

Четыре числа образуют геометрическую прогрессию. Если к ним прибавить соответственно 3, 12, 13 и 22, то получим четыре числа, образующие арифметическую прогрессию. Определи числа, образующие геометрическую прогрессию.

ответ:
знаменатель геометрической прогрессии: q=
.

Члены геометрической прогрессии:

b1=
b2=
b3=
b4=

Показать ответ

Ответ:

morfikk

11.10.2020 15:35

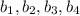Пуcть b_1, b_2, b_3, b_4 - члены геометрической прогрессии, 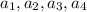a_1, a_2, a_3, a_4 - члены арифметической прогрессии.

Использовав формулу общего члена прогрессии, перепишем члены геометрической прогрессии в следующем виде: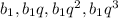 b_1, b_1q, b_1q^2, b_1q^3 .

По свойству арифметической прогрессии, каждый ее член равен среднему арифметическому двух соседних с ним членов:

$a_2=\frac{a_1+a_3}{2}$ , $a_3=\frac{a_2+a_4}{2}$ .

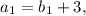
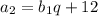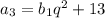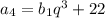По условию a_1=b_1+3, a_2=b_1q+12 , a_3=b_1q^2+13 , a_4=b_1q^3+22 .

Итого:

$2(b_1q+12)=b_1+3+b_1q^2+13;\\\\2(b_1q^2+13)=b_1q+12+b_1q^3+22$

Решаем систему:

$\left \{ {{2b_1q+24=b_1+b_1q^2+16} \atop {2b_1q^2+26=b_1q+b_1q^3+34}} \right. \\\\\left \{ {{2b_1q+8=b_1+b_1q^2} \atop {2b_1q^2-8=q(b_1q+b_1q^2)}} \right.\\\\\left \{ {{2b_1q+8=b_1+b_1q^2} \atop {2b_1q^2-8=q(2b_1+8)}} \right. \\\\\left \{ {{2b_1q+8=b_1+b_1q^2} \atop {2b_1q^2-8=2b_1q+8q}} \right. \\\\8q=-8\Rightarrow q=-1\\\\2b_1\cdot(-1)+8=b_1+b_1\cdot(-1)^2\\\\-2b_1+8=b_1+b_1\\\\4b_1=8\Rightarrow b_1=2$

Теперь мы можем вычислить члены геометрической прогрессии:

$b_1=2;\\\\b_2=b_1q=2\cdot(-1)=-2\\\\b_3=b_2q=-2\cdot(-1)=2\\\\b_3=b_3q=2\cdot(-1)=-2$

ОТВЕТ: 2; -2; 2; -2.

0,0(0 оценок)

Популярные вопросы: Алгебра

matyushin06

14.08.2021 23:08

тоьько пятое через 15 мин отдавать...

turdalievab

25.07.2020 07:19

Імовірність своєчасної сплати податків для підприємства А дорівнює а, для підприємства В дорівнює b, а для підприємства С дорівнює с. відомо, що є лише два підприємства своєчасно...

РЧВ21

22.09.2022 01:59

В кинотеатре «Аврора» билеты имеют базовую стоимость 182 рубл(-ей, -я, -ь). Также действует система скидок на билеты и имеются дополнительные бонусы. Время сеансаРазмер скидки, %...

Пропропрокакашку

13.06.2021 08:12

Не выполняя построений , найдите координаты точек пересечения графика функции y = -x+4...

динка84

25.02.2022 14:30

Знайдіть область визначення функції y=2x+1;y=...

Dasharozzz321

12.07.2021 20:58

Решите алгебраическим методом все три системы...

YUSUFOV

31.05.2021 13:05

Вызначите последньюю цифру числа 9 в 2018 степени. просто цифру!...

megan99

11.02.2021 11:24

Вромбе abcd угол abc равен 56 градусов. найдите угол acd. ответ дайте в градусах. (ответ будет 62? )...

galstyangevorgp08o0o

20.06.2022 22:38

Прямаяy=kx+bпересекает ось oxв точке (18; 0), а ось oy — в точке (0; 9). запишите уравнение этой прямой...

lybabibrka

20.06.2022 22:38

Сторона основания правильной четырехугольной пирамиды равна 5 а площадь ее полной поверхности равна 85. найдите угол наклона боковой грани к плоскости основания. с этой...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку