или
Объяснение:
Модуль раскрывается двумя вариантами: со знаком + или со знаком - . В этой задаче 2 модуля, следовательно максимум может быть 4 раскрытия.
На практике имеем 3 области:
Область не существует, т.к. нет пересечений у неравенств, задающих область.
Рассмотрим каждый из трех случаев:
Получили решение, лежащее в области:
Получили неравенство, выполненное для любого x из этой области. Следовательно решение в этой области - сама область:
"Сшиваем" полученные решение и получаем:
6х-18=12
6х=30
х=5
2. 14=7(х+2)
14=7х+14
7х=0
х=0
3. 12х+4=3(4х-2)
12х+4=12х-6
10 ≠ 0
нет решения
4. 3х +(2х-1) =10
3x + 2x-1=10
5x=9
x= 9/5
x= 1 4/5
х= 1,8
5. (3х-2) - (х-1)=10
3x-2-x+1=10
2х=11
x= 11/2
x= 5,5
6. 2(x-1)-4=6(x+2)
2x-2-4=6x+12
-4x=18
x= -18/4
x= -4,5
7. 6x-3(x-1)=4+5x
6x-3x+3=4+5x
-2x=1
x= -1/2
x= -0,5
8. 5x+18=7x+6(3x-7)
5x+18= 7x+18x-42
42+18=7x+18x-5x
60=20x
x= 20/60
х= 1/3
9. 12+4(х-3)-2х=(5-3х)+9
12+4х-12-2х= 5-3х+9
2х=14-3х
5х=14
х=14/5
х=2,8
10. 3х-7(3х-4)=5(2х-7)
3х-21х +28= 10х-35
28+35=10х+21х-3х
63= 28х
х= 28/63
х= 4/9
Объяснение:
Модуль раскрывается двумя вариантами: со знаком + или со знаком - . В этой задаче 2 модуля, следовательно максимум может быть 4 раскрытия.
На практике имеем 3 области:
Область не существует, т.к. нет пересечений у неравенств, задающих область.
не существует, т.к. нет пересечений у неравенств, задающих область.
Рассмотрим каждый из трех случаев:
Получили решение, лежащее в области: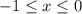
Получили неравенство, выполненное для любого x из этой области. Следовательно решение в этой области - сама область: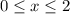
Получили решение, лежащее в области: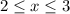
"Сшиваем" полученные решение и получаем: