34. Найдите длину стороны куба, объем которого равен прямоугольного параллелепипеда с измерениями: 1) 4 см, 6см и 9 см 2)4см,10см,25см 3)5см,8см,25см 4) 27 см,8см,125см. 5)6,4см, 2,7см,34,3 см ,6)0,7 см,4,9см,0,8см
Рассмотрим событие – из наугад выбранной радиостанции передают самолету один и тот же сигнал. Данное событие может произойти или не произойти в результате осуществления одной из следующих гипотез:
Рассмотрим 3 случая: с отрицательной, нулевой и положительной правой частью.
1. Если , то есть .
Тогда предполагается, что модуль должен принимать значения, не большие некоторого отрицательного, то есть тоже отрицательные. Но модуль не может принимать отрицательных значений. Значит, в этом случае неравенство решений не имеет.
2. Если , то есть .
Получаем неравенство:
Поскольку модуль не принимает отрицательных значений, достаточно решить уравнение:
3. Если , то есть , то получаем неравенство с положительной правой частью:
Відповідь:
Пояснення:
А - самолет получит посылаемый сигнал.
Рассмотрим событие – из наугад выбранной радиостанции передают самолету один и тот же сигнал. Данное событие может произойти или не произойти в результате осуществления одной из следующих гипотез:
В1– будет выбрана 1-я радиостанция;
В2– будет выбрана 2-я радиостанция;
В3– будет выбрана 3-я радиостанция.
Р(В1) =Р(В2) =Р(В3) =1/3
Р В₁(А) =0,8; Р В₂(А) =0,7; Р В₃(А) =0,6;
По формуле полной вероятности:
P(A) =Р(В1)*Р В₁(А) +Р(В2)*Р В₂(А) + Р(В3) *Р В₃(А) =1/3*(0,8+0,7+0,6)= 0,7
Рассмотрим 3 случая: с отрицательной, нулевой и положительной правой частью.
1. Если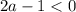 , то есть
, то есть 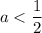 .
.
Тогда предполагается, что модуль должен принимать значения, не большие некоторого отрицательного, то есть тоже отрицательные. Но модуль не может принимать отрицательных значений. Значит, в этом случае неравенство решений не имеет.
2. Если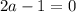 , то есть
, то есть 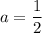 .
.
Получаем неравенство:
Поскольку модуль не принимает отрицательных значений, достаточно решить уравнение:
3. Если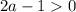 , то есть
, то есть 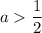 , то получаем неравенство с положительной правой частью:
, то получаем неравенство с положительной правой частью:
Заменим его следующим двойным неравенством:
Таким образом получаем ответ:
при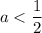 : решений нет
: решений нет
при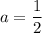 :
: 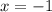
при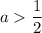 :
: ![x\in[-2a;\ 2a-2]](/tpl/images/2004/6663/9d563.png)