-2x^2+3x+9<0 2x^2-x+4>0 -x^2+3x-8>0

1) f(x) = x^2 - 6x + 5

D(f) = R

1) Знайдемо проміжки монотоності:

f`(x) = 2x - 6 = 2(x - 3)

f`(x) = 0

2(x - 3) = 0

x = 3

(дивись малюнок)

f(x) спадає якщо х ∈ (-∞; 3) і зростає якщо х ∈ (3; +∞)

2) знайдемо точки екстремума.

х(min) = 3 ⇒   y(min) = 3² - 6 * 3 +5 = 9 - 18 + 5 = -4

точки max не існеє.

2) f(x) = x^4 - 2x^2

D(f) = R

1) Знайдемо проміжки монотоності:

f`(x) = 4x³ - 4х = 4х(x² - 1) = 4х(х - 1)(х + 1)

f`(x) = 0

4х(х - 1)(х + 1) = 0

х = 0,  х = 1,  х = -1

(дивись малюнок)

f(x) спадає якщо х ∈ (-∞; -1) і (0; 1);

 зростає якщо х ∈ (-1; 0) і (1; +∞)

2) знайдемо точки екстремума.

х(min) = -1 ⇒   y(min) = (-1)⁴ - 2 * (-1)²  = 1 - 2 = -1

х(min) = 1 ⇒   y(min) = 1⁴ - 2 * 1²  = 1 - 2 = -1

 х(max) = 0 ⇒   y(max) = 0⁴ - 2 * 0²  = 0

Множества значений синуса: [-1;1], поэтому наибольшим число будет b=9,5 далее будет c=2,5.

Сравним a и d:

На тригонометрической окружности π это половина круга, а  синус угла это его проекция на ось ординат;

π ≈ 3,14  ⇒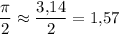  

На самом деле π чуть больше 3,14 поэтому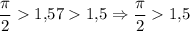 , то есть 1,5 лежит в 1 четверти ближе к границе со 2 четвертью.

Определим примерное положение 9,5.

9,5 - 3·3,14 = 0,50-0,42 = 0,08

π = 3,141... Поэтому 9,5-3·π > 0,08-(3·0,002) = 0,074

Таким образом на окружности 9,5 ∈ (π+0,074 ; π+0,08), то есть лежит в 3 четверти, ближе к границе со 2 четвертью.

Сравнение синусов смотри в приложении.

ответ: b, c, d и a.