115. Составьте, если возможно, пропорцию из чисел: 1) 3; 4; 2; 6; 2) 2; 3; 6; 9; 3) 4; 5; 15; 12; 4) 0,6; 1,5; 2; 5.

Показать ответ

Ответ:

solovyovaolena

15.04.2022 04:28

Дано:

Правильная четырёхугольная пирамида FABCD.

S (основания) = 9 (см²).

FG = h = 12 (см).

Найти:

FH = ? (см).

Решение:

"В основании правильной четырёхугольной пирамиды лежит квадрат".

⇒ ABCD - квадрат. Чтобы найти сторону основания, нужно подобрать такое число, которое при возведении числа во 2 степень даёт ответ 9. Это число 3 ⇒ AB = BC = CD = DA = 3 (см).

Проведём из вершины F к стороне основания апофему FH, которая по свойству делит сторону основания пополам.

⇒ DH = HC = 3 : 2 = 1,5 (см).

Проведём из точки G к точке H отрезок. Внутри пирамиды образовался прямоугольный △FGH, где FG - катет прямоугольного треугольника (высота пирамиды), GH - катет прямоугольного треугольника, FH - гипотенуза прямоугольного треугольника (апофема пирамиды).

По свойству катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырёхугольной пирамиды.

⇒ DH = HC = GH = 1,5 (см).

Так как апофема FH является ещё и гипотенузой прямоугольного треугольника FGH, то найдём её по т.Пифагора (c = √(a² + b²), где c - гипотенуза, a и b - катеты).

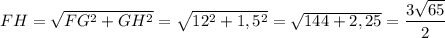$FH = \sqrt{FG^2+ GH^2} = \sqrt{12^2 + 1,5^2} = \sqrt{144 + 2,25} =\dfrac{3\sqrt{65}}{2}$ (см).

ответ: $\Large{\boxed{\dfrac{3\sqrt{65}}{2}}}$ (см).
В правильной четырёхугольной пирамиде площадь основания равна 9 см2, а высота пирамиды равна 12 см.