рассмотрим первый группа средний рост 180 это средняя арифмитическая если предположить что группа состоит из 6 человек то сумма всех возрастов 180×6=1080 см если половина группы имеют минимальный рост 175 см то их суума равна 525 см значит на остальных отходит 1080-525=555 см на троих остальных то их рост равен 185 см если рассмотеть случай максимальной допустимой нормы то рост троих 190×3=570 см а значит на остальных отходит 1080-570=510 см 510÷3=170 а это значит при максимальной норме значение роста более приближенны рассмотрев взяв за моду крайние точки периода мы можем сделать вывод что годны 3/4 полка к службе
второй случай максимальный рост 189 см это нам ничто не дает так как могут быть 150 см 160 см то есть условиям не подходящие а значит вторая группа вряд ли годна службе
третий случай медианна 176 но опять же нет гарантии что роста входят в этот промежуток
может ряд 150 160 176 195 200 а это значит что третий случай тоже не подойдет и всего этого только первыя группа годна службе
Это функция представляет из себя ломанную, нам надо найти нули этой функции. На числовой прямой отметим точки в которых аргументы модулей равны нулю. Таким образом мы сможем узнать как на промежутках раскрываются модули и выглядит функция, сверху напишу модули, чтобы было понятно, хотя можно сразу писать конечную функцию для промежутка. см. вниз.
Да и ||2x-1|-5| я представил как |2x-6| и |-2x-4|, при этом первый существует когда x>0.5, а другой когда x<0.5 т.к. 2x-1=0 =>x=0.5
Ординаты точек в которых происходит смена знака у модуля.
Можно построить график ломанной, а можно сразу по условию определить где функция будет равна 0.
Главное помнить, что функция существует на каком-то промежутку, а не при всех х.
рассмотрим первый группа средний рост 180 это средняя арифмитическая если предположить что группа состоит из 6 человек то сумма всех возрастов 180×6=1080 см если половина группы имеют минимальный рост 175 см то их суума равна 525 см значит на остальных отходит 1080-525=555 см на троих остальных то их рост равен 185 см если рассмотеть случай максимальной допустимой нормы то рост троих 190×3=570 см а значит на остальных отходит 1080-570=510 см 510÷3=170 а это значит при максимальной норме значение роста более приближенны рассмотрев взяв за моду крайние точки периода мы можем сделать вывод что годны 3/4 полка к службе
второй случай максимальный рост 189 см это нам ничто не дает так как могут быть 150 см 160 см то есть условиям не подходящие а значит вторая группа вряд ли годна службе
третий случай медианна 176 но опять же нет гарантии что роста входят в этот промежуток
может ряд 150 160 176 195 200 а это значит что третий случай тоже не подойдет и всего этого только первыя группа годна службе
ответ 1 группа
Это функция представляет из себя ломанную, нам надо найти нули этой функции. На числовой прямой отметим точки в которых аргументы модулей равны нулю. Таким образом мы сможем узнать как на промежутках раскрываются модули и выглядит функция, сверху напишу модули, чтобы было понятно, хотя можно сразу писать конечную функцию для промежутка. см. вниз.
Да и ||2x-1|-5| я представил как |2x-6| и |-2x-4|, при этом первый существует когда x>0.5, а другой когда x<0.5 т.к. 2x-1=0 =>x=0.5
Ординаты точек в которых происходит смена знака у модуля.
Можно построить график ломанной, а можно сразу по условию определить где функция будет равна 0.
Главное помнить, что функция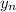
существует на каком-то промежутку, а не при всех х.
ответ: x∈[0.5;3].