1) Найдите десятый член арифметической
прогрессии -8; -6,5; -5… Вычислите сумму первых
десяти ее членов.
2) Найдите восьмой член геометрической прогрессии
3) Сумма третьего и шестого членов арифметической
прогрессии равна 3. Второй ее член на 15 больше
седьмого. Найдите первый и второй члены этой
прогрессии.
4) Найдите х, при котором числа х - 1, 2х - 1, х 2 - 5
составляют арифметическую прогрессию;

(см. объяснение)

Объяснение:

Самый верный решить любой параметр - это постараться построить его в координатах (b; x).

Попробуем применить этот прием здесь.

Сначала заметим, что при равенство неверно при любом значении параметра. Тогда на протяжении решения при необходимости будем спокойно делить на .

Раскроем :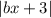

Видим гиперболу в координатах (b; x).

Построим ее и просчитаем знаки в областях, которые она образует, подставляя координаты соответствующих точек в .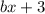

Тогда при :

Строим фрагмент этого графика в определенных выше областях.

При :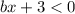

Тоже строим фрагмент этого графика в определенных выше областях.

Получим график уравнения:

(см. прикрепленный файл)

Итого:

При уравнение не имеет корней.При уравнение имеет единственный корень.При уравнение имеет ровно два различных корня.

Задание выполнено!

|bx + 3| = 5x

При x ≥ 0 возводим обе части уравнения в квадрат.

|bx + 3|² = (5x)²   ⇔   (bx + 3)² = (5x)²   ⇒  (bx + 3)² - (5x)² = 0

(bx + 3 - 5x)(bx + 3 + 5x) = 0

bx + 3 - 5x = 0   ⇒  x(b - 5) = -3

Если b = 5, то уравнение, то 0x = -3, уравнение решений не имеет, если b ≠ 5 и то уравнение имеет корень x = 3/(5-b) и причём имеет корень, когда 3/(5-b) ≥ 0 откуда b<5, а при b > 5 не имеет корень

bx + 3 + 5x = 0   ⇒  x(b + 5) = -3

Если b = -5, то -10x = -3 ⇒ x=3/10. Если b ≠ -5, то уравнение имеет корень x = -3/(b+5), причём имеет корень, когда -3/(b+5)≥0, то есть, при b<-5, а при b > -5 корень не имеет.

при b ≥ 5 уравнение корней не имеетпри -5 ≤ b < 5 уравнение имеет один кореньпри b < -5 уравнение имеет два различных корня.